题目内容
化简f（x）=cos（π+2x）+cos（π-2x）+2（x∈R，k∈Z），并求函数f（x）的值域和最小正周期．分析：先利用诱导公式和两角和公式对函数解析式进行化简的f（x）=4cos2x，进而根据余弦函数的单调性求得f（x）的值域和最小正周期．
解答：解：f（x）=cos（π+2x）+cos（π-2x）+2=2cos（
+2x）+2
sin（
+2x）=4cos2x
所以函数f（x）的值域为[-4，4]，
最小正周期T=
=π．
| π |
| 3 |
| 3 |
| π |
| 3 |
所以函数f（x）的值域为[-4，4]，
最小正周期T=
| 2π |
| ω |
点评：本题主要考查了利用诱导公式和两角和公式进行化简求值．涉及了函数的值域，三角函数的周期性等问题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
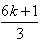π+2x）+cos（
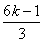π-2x）+2
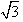sin（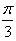
+2x）（x∈R，k∈Z），并求函数f（x）的值域和最小正周期。