题目内容
13.若a>0且a≠1,且loga(2a+1)<loga3a<0,求a的取值范围.分析 利用函数的单调性求解,分当a>1时,不成立,当0<a<1时,原不等式可转化为2a+1>3a>1求解,两种结果取并集.
解答 解:当a>1时,loga(2a+1)>0,loga3a>0,
原不等式不成立,
当0<a<1时,原不等式可转化2a+1>3a>1.
解得:$\frac{1}{3}$<a<1,
综上,a的取值范围是:($\frac{1}{3}$,1).
点评 本题主要考查利用函数单调性定义解抽象不等式,一般来讲,抽象不等式的解法是利用函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列计算正确的是( )
| A. | xm•x3=x3m | B. | (-4a3)2=4a6 | C. | (-x2)3=-x6 | D. | -(-m2)4=m8 |
8.已知定义域为R的偶函数f(x)在(-∞,0]是减函数,若f($\frac{1}{2}$)=0,则不等式f(log4x)<0的解集是( )
| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,2) | C. | (2,+∞) | D. | ($\frac{1}{2}$,1)∪(2,+∞) |
18.已知实数x,一满足$\left\{\begin{array}{l}{y≥\frac{x}{3}-2}\\{y≤2x+4}\\{2x+3y-12≤0}\end{array}\right.$,直线(2+λ)x-(3+λ)y+(1-2λ)=0(λ∈R)过定点A(x0,y0),则$\frac{y-{y}_{0}}{x-{x}_{0}}$的取值范围为( )
| A. | [$\frac{1}{5}$,7] | B. | [$\frac{1}{7}$,5] | C. | (-∞,$\frac{1}{5}$]∪[7,+∞] | D. | (-∞,$\frac{1}{7}$]∪[5,+∞] |
9.设集合A={x|x≤1},B={x|x>p},要使A∩B=∅,则p应满足的条件是( )
| A. | p<1 | B. | p≤1 | C. | p>1 | D. | p≥1 |
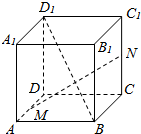 如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.
如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.