题目内容
18.已知实数x,一满足$\left\{\begin{array}{l}{y≥\frac{x}{3}-2}\\{y≤2x+4}\\{2x+3y-12≤0}\end{array}\right.$,直线(2+λ)x-(3+λ)y+(1-2λ)=0(λ∈R)过定点A(x0,y0),则$\frac{y-{y}_{0}}{x-{x}_{0}}$的取值范围为( )| A. | [$\frac{1}{5}$,7] | B. | [$\frac{1}{7}$,5] | C. | (-∞,$\frac{1}{5}$]∪[7,+∞] | D. | (-∞,$\frac{1}{7}$]∪[5,+∞] |
分析 由约束条件作出可行域,由直线系方程求出直线所过定点A,结合图形由两点求斜率得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{y≥\frac{x}{3}-2}\\{y≤2x+4}\\{2x+3y-12≤0}\end{array}\right.$作出可行域如图,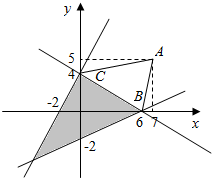
由(2+λ)x-(3+λ)y+(1-2λ)=0,得(2x-3y+1)+λ(x-y-2)=0,
联立$\left\{\begin{array}{l}{2x-3y+1=0}\\{x-y-2=0}\end{array}\right.$,解得A(7,5),
∴直线(2+λ)x-(3+λ)y+(1-2λ)=0(λ∈R)过定点A(7,5),
$\frac{y-{y}_{0}}{x-{x}_{0}}$即$\frac{y-5}{x-7}$的几何意义为可行域内的动点(x,y)与定点A(7,5)连线的斜率.
由图可知:${k}_{AB}=\frac{5-0}{7-6}=5$,${k}_{AC}=\frac{5-4}{7-0}=\frac{1}{7}$,
∴$\frac{y-{y}_{0}}{x-{x}_{0}}$的取值范围为[$\frac{1}{7},5$].
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
9.已知集合E={x|-3<x<2},F={x|0≤x≤4},则E∪F等于( )
| A. | A{x|-3<x≤4} | B. | {x|0≤x<2} | C. | {x|2<x≤4} | D. | {x|-3<x≤0} |
10.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知cosB=-$\frac{1}{2}$.
(1)求sinAsinC的取值范围;
(2)若b=2$\sqrt{3}$,求△ABC面积的最大值.
(1)求sinAsinC的取值范围;
(2)若b=2$\sqrt{3}$,求△ABC面积的最大值.
14.函数y=sin($\frac{π}{3}$-2x)的单调减区间是( )
| A. | [2kπ-$\frac{π}{12}$,2kπ+$\frac{5π}{12}$](k∈Z) | B. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | ||
| C. | [2kπ+$\frac{5π}{12}$,2kπ+$\frac{11π}{12}$](k∈Z) | D. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) |