题目内容
设数列 的前项n和为
的前项n和为 ,若对于任意的正整数n都有
,若对于任意的正整数n都有 .
.
(1)设 ,求证:数列
,求证:数列 是等比数列,并求出
是等比数列,并求出 的通项公式。(2)求数列
的通项公式。(2)求数列 的前n项和.
的前n项和.
解:(1) 对于任意的正整数都成立,
对于任意的正整数都成立, 
两式相减,得 ∴
∴ , 即
, 即
 ,即
,即 对一切正整数都成立。∴数列
对一切正整数都成立。∴数列 是等比数列。
是等比数列。
由已知得  即
即
∴首项 ,公比
,公比 ,
, 。
。 。
。


练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
若 ,
, ,
, 均为单位向量,且
均为单位向量,且 ,
, ,则
,则 的最大值为( )
的最大值为( )
|
| A. |
| B. | 1 | C. |
| D. | 2 |
 位回文数有_________个.
位回文数有_________个. 中,“
中,“ ”是“
”是“ ”的充要条件;
”的充要条件; 为等比数列,且
为等比数列,且 ; ③不等式
; ③不等式 的解集为
的解集为 ;
; 上一点,
上一点, 分别是双曲线的左、右焦点,且
分别是双曲线的左、右焦点,且 其中真命题的序号为_____________.(把正确的序号都填上)
其中真命题的序号为_____________.(把正确的序号都填上)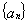 的前
的前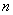 项和
项和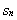 满足
满足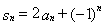 ,
,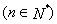 (1)求数列
(1)求数列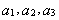
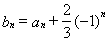 ,求证:数列
,求证:数列 为等比数列,并指出
为等比数列,并指出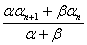 ,n∈N*,其中常数α,β均为非零实数,且α+β≠0.
,n∈N*,其中常数α,β均为非零实数,且α+β≠0.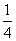 , a1=1,a2=
, a1=1,a2=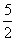 ,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+
,求证:数列{| an+1-an-1|} (n∈N*,n≥2)与数列{n+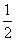 } (n∈N*)中没有相同数值的项.
} (n∈N*)中没有相同数值的项.  的图像经过点
的图像经过点 和
和 ,令
,令 ,记数列的前项和为
,记数列的前项和为 ,当
,当 时,
时, 的值等于A .
的值等于A .  B.
B.  C.
C.  D.
D. 
 的前
的前 项和为
项和为 ,若
,若 ,且满足
,且满足 ,则使
,则使 的
的
