题目内容
利用定义法证明:函数f(x)=x2在区间(0,+∞)上为增函数.
分析:可设0<x1<x2,由已知函数的解析式,利用定义法进行判断.
解答:解:由题意可以设0<x1<x2,
则f(x1)-f(x2)=x12-x22=(x1+x2)(x1-x2),
∵0<x1<x2,∴x1+x2>0,x1-x2<0,
∴(x1+x2)(x1-x2)<0,
∴f(x1)<f(x2),
∴f(x)在区间(0,+∞)上为增函数.
则f(x1)-f(x2)=x12-x22=(x1+x2)(x1-x2),
∵0<x1<x2,∴x1+x2>0,x1-x2<0,
∴(x1+x2)(x1-x2)<0,
∴f(x1)<f(x2),
∴f(x)在区间(0,+∞)上为增函数.
点评:本题考查函数的单调性的判断与证明,属基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
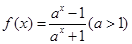 .
. 是
是 上的增函数
上的增函数 .
. 是
是 上的增函数
上的增函数