ЬтФПФкШн
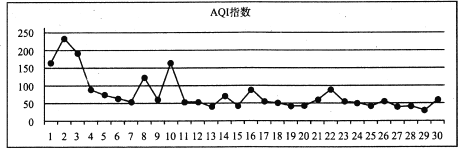
ЁОЬтФПЁПФГЛЈЦдЮЊЬсИпФГЦЗжжЛЈУчжЪСПЃЌПЊеЙММЪѕДДаТЛюЖЏЃЌдк![]() ЪЕбщЕиЗжБ№гУМзЁЂввЗНЗЈХрбЕИУЦЗжжЛЈУч.ЮЊЙлВтЦфЩњГЄЧщПіЃЌЗжБ№дкЪЕбщЕиЫцЛњГщШЁИї
ЪЕбщЕиЗжБ№гУМзЁЂввЗНЗЈХрбЕИУЦЗжжЛЈУч.ЮЊЙлВтЦфЩњГЄЧщПіЃЌЗжБ№дкЪЕбщЕиЫцЛњГщШЁИї![]() жъЃЌЖдУПжъНјаазлКЯЦРЗжЃЌНЋУПжъЫљЕУЕФзлКЯЦРЗжжЦГЩШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.МЧзлКЯЦРЗжЮЊ
жъЃЌЖдУПжъНјаазлКЯЦРЗжЃЌНЋУПжъЫљЕУЕФзлКЯЦРЗжжЦГЩШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.МЧзлКЯЦРЗжЮЊ![]() МАвдЩЯЕФЛЈУчЮЊгХжЪЛЈУч.
МАвдЩЯЕФЛЈУчЮЊгХжЪЛЈУч.

![]() ЧѓЭМжа
ЧѓЭМжа![]() ЕФжЕЃЌВЂЧѓзлКЯЦРЗжЕФжаЮЛЪ§.
ЕФжЕЃЌВЂЧѓзлКЯЦРЗжЕФжаЮЛЪ§.
![]() гУбљБОЙРМЦзмЬхЃЌвдЦЕТЪзїЮЊИХТЪЃЌШєдк
гУбљБОЙРМЦзмЬхЃЌвдЦЕТЪзїЮЊИХТЪЃЌШєдк![]() СНПщЪдбщЕиЫцЛњГщШЁ
СНПщЪдбщЕиЫцЛњГщШЁ![]() ПУЛЈУчЃЌЧѓЫљГщШЁЕФЛЈУчжаЕФгХжЪЛЈУчЪ§ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЛ
ПУЛЈУчЃЌЧѓЫљГщШЁЕФЛЈУчжаЕФгХжЪЛЈУчЪ§ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЛ
![]() ЬюаДЯТУцЕФСаСЊБэЃЌВЂХаЖЯЪЧЗёга
ЬюаДЯТУцЕФСаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊгХжЪЛЈУчгыХрг§ЗНЗЈгаЙи.
ЕФАбЮеШЯЮЊгХжЪЛЈУчгыХрг§ЗНЗЈгаЙи.
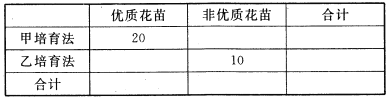
ИНЃКЯТУцЕФСйНчжЕБэНіЙЉВЮПМ.
![]()
ЃЈВЮПМЙЋЪНЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() .ЃЉ
.ЃЉ
ЁОД№АИЁПЃЈ1ЃЉ82.5ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉга![]() ЕФАбЮеШЯЮЊгХжЪЛЈУчгыХрг§ЗНЗЈгаЙиЯЕ.
ЕФАбЮеШЯЮЊгХжЪЛЈУчгыХрг§ЗНЗЈгаЙиЯЕ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦЕТЪжЎКЭЮЊ1ЕУЕН![]() ЃЌИљОнУцЛ§ЯрЕШЃЌЧѓГіжаЮЛЪ§.
ЃЌИљОнУцЛ§ЯрЕШЃЌЧѓГіжаЮЛЪ§.
ЃЈ2ЃЉРћгУЖўЯюЗжВМСаГіЖдгІЕФИХТЪЃЌаДГіЗжВМСаЃЌЫуГіЪ§бЇЦкЭћ.
ЃЈ3ЃЉИљОнгХжЪЛЈУчПХЪ§ЃЌЬюКУБэИёЃЌбЁШЁЯргІЪ§ОнЃЌМЦЫуЕУЕН![]() ЃЌдйНјааХаЖЯ.
ЃЌдйНјааХаЖЯ.
![]() гЩ
гЩ![]() ЃЌ
ЃЌ
НтЕУ![]()
СюЕУЗжжаЮЛЪ§ЮЊ![]() ЃЌгЩ
ЃЌгЩ![]() НтЕУ
НтЕУ![]()
ЙЪзлКЯЦРЗжЕФжаЮЛЪ§ЮЊ![]()
![]() гЩ
гЩ![]() гыЦЕТЪЗжВМжБЃЌгХжЪЛЈУчЕФЦЕТЪЮЊ
гыЦЕТЪЗжВМжБЃЌгХжЪЛЈУчЕФЦЕТЪЮЊ![]() ЃЌМДИХТЪЮЊ
ЃЌМДИХТЪЮЊ![]() ЃЌ
ЃЌ
ЩшЫљГщШЁЕФЛЈУчЮЊгХжЪЛЈУчЕФПХЪ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌгкЪЧЃЌ
ЃЌгкЪЧЃЌ
![]()
![]() ЦфЗжВМСаЮЊЃК
ЦфЗжВМСаЮЊЃК

ЫљвдЃЌЫљГщШЁЕФЛЈУчЮЊгХжЪЛЈУчЕФЪ§бЇЦкЭћ![]()
![]() НсКЯ
НсКЯ![]() гыЦЕТЪЗжВМжБЗНЭМЃЌгХжЪЛЈУчЕФЦЕТЪЮЊ
гыЦЕТЪЗжВМжБЗНЭМЃЌгХжЪЛЈУчЕФЦЕТЪЮЊ![]() ЃЌдђбљБОжжЃЌгХжЪЛЈУчЕФПХЪ§ЮЊ
ЃЌдђбљБОжжЃЌгХжЪЛЈУчЕФПХЪ§ЮЊ![]() ПУЃЌСаСЊБэШчЯТБэЫљЪОЃК
ПУЃЌСаСЊБэШчЯТБэЫљЪОЃК

ПЩЕУ![]()
ЫљвдЃЌга![]() ЕФАбЮеШЯЮЊгХжЪЛЈУчгыХрг§ЗНЗЈгаЙиЯЕ.
ЕФАбЮеШЯЮЊгХжЪЛЈУчгыХрг§ЗНЗЈгаЙиЯЕ.