题目内容

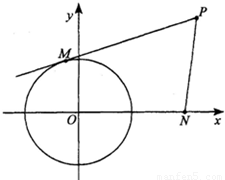
如图，已知点N（2，0）和圆O：x²+y²=1．过动点P作圆O的切线PM（M为切点），若|PM|= $数学公式$ |PN|，求动点P的轨迹方程．

解：连接MO，PO，设P（x，y），
在Rt△OMP中，|PM|²=|OP|²-|OM|²，所以|PM|²=x²+y²-1，
根据|PM|= $\text{[math]}$ |PN|，得x²+y²-1=2[（x-2）²+y²]，∴x²+y²-8x+9=0，
∴动点P的轨迹方程x²+y²-8x+9=0．
分析：在Rt△OMP中，利用|PM|²=|OP|²-|OM|²，得|PM|²=x²+y²-1，根据|PM|= $\text{[math]}$ |PN|，可求轨迹方程．
点评：本题主要考查轨迹方程的求解，关键是挖掘隐含，充分利用条件进行转换．

练习册系列答案

王朝霞小升初重点校系列答案

专项卷和真题卷系列答案

文曲星中考总复习系列答案

问题引领系列答案

先锋题典系列答案

知识大集结系列答案

随堂口算系列答案

小学升学夺冠系列答案

培优好题系列答案

培优60课系列答案

相关题目

如图，已知点A（-2，0），点P是⊙B：（x-2）²+y²=36上任意一点，线段AP的垂直平分线交BP于点Q，点Q的轨迹记为曲线C．
（Ⅰ）求曲线C的方程；
（Ⅱ）已知⊙O：x²+y²=r²（r＞0）的切线l总与曲线C有两个交点M、N，并且其中一条切线满足∠MON＞90°，求证：对于任意一条切线l总有∠MON＞90°．

如图，已知点N（2，0）和圆O：x²+y²=1．过动点P作圆O的切线PM（M为切点），若|PM|=

|PN|，求动点P的轨迹方程．

（2007•深圳二模）如图，已知点C（-2，0），直线l₀：x=-4与x轴交于点A，动点P到直线l₀的距离为d，且d=

PC．
（Ⅰ）求动点P的轨迹E的方程；
（Ⅱ）设过点A的直线l交轨迹于M、N两点，且CN⊥CN，求直线l的方程．

如图，已知点N（2，0）和圆O：x²+y²=1．过动点P作圆O的切线PM（M为切点），若|PM|=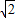

|PN|，求动点P的轨迹方程．