题目内容
【题目】已知f（x）的定义在（0，3）上的函数，f（x）的图象如图所示，那么不等式f（x）cosx＜0的解集是（ ）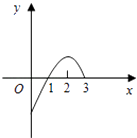 
A.（0，1）∪（2，3）
B.
C.
D.（0，1）∪（1，3）
【答案】C
【解析】解：由函数图象可知：当f（x）＜0时，0＜x＜1；当f（x）＞0时，1＜x＜3；
而cosx中的x∈（0，3），当cosx＞0时，x∈（0， 
）；当cosx＜0时，x∈（ ，3），
则f（x）cosx＜0，可化为： 
或 
即 
或 
，
解得： ＜x＜3或0＜x＜1，
所以所求不等式的解集为：（0，1）∪（ ，3），
故选C．
【考点精析】本题主要考查了函数的图象和余弦函数的单调性的相关知识点，需要掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值；余弦函数的单调性：在
上是增函数；在
上是减函数才能正确解答此题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
