题目内容
如图所示,三棱柱ABC A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=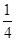 AB.
AB.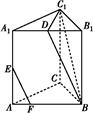
(1)求证:EF∥平面BC1D;
(2)在棱AC上是否存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1∶15,若存在,指出点G的位置;若不存在,说明理由.
(1)见解析 (2) 不存在.理由见解析
解析(1)证明:取AB的中点M,
∵AF=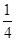 AB,
AB,
∴F为AM的中点,
又∵E为AA1的中点,
∴EF∥A1M.
在三棱柱ABC A1B1C1中,D、M分别为A1B1、AB的中点,
A1B1C1中,D、M分别为A1B1、AB的中点,
∴A1D∥BM,A1D=BM,
∴四边形A1DBM为平行四边形,
∴A1M∥BD,
∴EF∥BD,
∵BD⊆平面BC1D,EF?平面BC1D,
∴EF∥平面BC1D.
(2)解:设AC上存在一点G,使得平面EFG将三棱柱分割成两部分的体积之比为1∶15,
则 ∶
∶ =1∶16,
=1∶16,
∵ =
=
=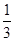 ×
×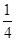 ×
×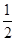 ×
×
= ·
· .
.
∴ ·
· =
= ,
,
∴ =
= ,
,
∴AG= AC>AC.
AC>AC.
所以符合要求的点G不存在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,已知
中,已知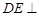 平面
平面 ,
,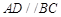 ,
,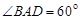 ,
,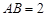 ,
,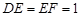 .
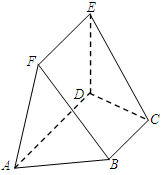
.
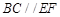 ;
;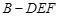 的体积.
的体积.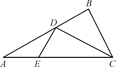 图①
图①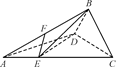 图②
图②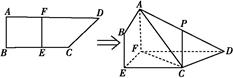
 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
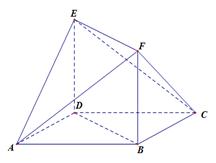
 是菱形,
是菱形, 是矩形,
是矩形, 面
面 ,
,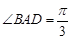 .
.
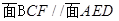 ;
;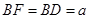 ,求四棱锥
,求四棱锥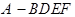 的体积.
的体积.


 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.