题目内容
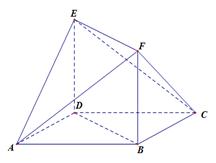
如图所示的多面体中,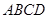 是菱形,
是菱形,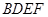 是矩形,
是矩形, 面
面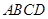 ,
,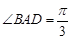 .
.
(1)求证:平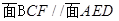 ;
;
(2)若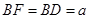 ,求四棱锥
,求四棱锥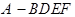 的体积.
的体积.
(1)证明过程详见解析;(2)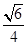 .
.
解析试题分析:
(1)根据面面平行的判断,要证明平面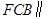 平面AED,只需要证明面FCB内两条相交的直线FB,BC与面AED平行,而BF与ED平行,BC与AD平行,即可得到两相交直线都与面AED平行,进而得到面面平行.
平面AED,只需要证明面FCB内两条相交的直线FB,BC与面AED平行,而BF与ED平行,BC与AD平行,即可得到两相交直线都与面AED平行,进而得到面面平行.
(2)要求的四棱锥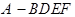 的体积,必须求的底面BDEF的面积与高,根据
的体积,必须求的底面BDEF的面积与高,根据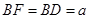 、BDEF为矩形可以求的底面积,由于面BDEF与面ABCD是垂直的(DE垂直与底面ABCD),所以可以连接AC与BD交于O,得到AO即为四棱锥的高.可以通过底面为有一个角为60度的菱形求的三角形ABD为等边三角形进而得到高AO的长度,再利用四棱锥的体积公式
、BDEF为矩形可以求的底面积,由于面BDEF与面ABCD是垂直的(DE垂直与底面ABCD),所以可以连接AC与BD交于O,得到AO即为四棱锥的高.可以通过底面为有一个角为60度的菱形求的三角形ABD为等边三角形进而得到高AO的长度,再利用四棱锥的体积公式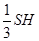 ,就求的了四棱锥的体积。
,就求的了四棱锥的体积。
试题解析:
(1)由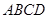 是菱形
是菱形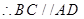
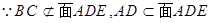
 3分
3分
由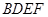 是矩形
是矩形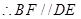


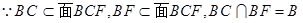
 6分
6分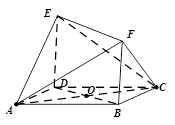
(2)连接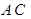 ,
,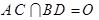
由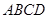 是菱形,
是菱形,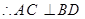
由 面
面 ,
,
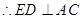
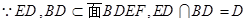
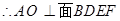 , 10分
, 10分
则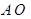 为四棱锥
为四棱锥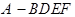 的高
的高
由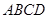 是菱形,
是菱形,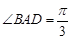 ,
,
则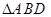 为等边三角形,
为等边三角形,
由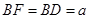 ;则
;则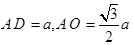
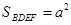 ,
,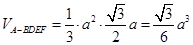 14分
14分
考点:面面平行的证明 线面平行 二面角 直二面角 坐标法

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,M是线段AE上的动点.
,M是线段AE上的动点.
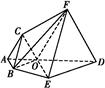
 OBED的体积.
OBED的体积.
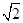 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积. A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=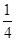 AB.
AB.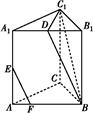
 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
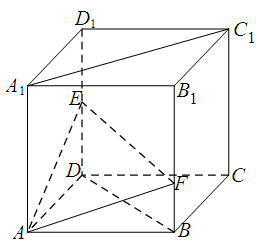
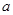 的正方体
的正方体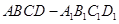 中,点
中,点 是棱
是棱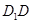 的中点,点
的中点,点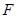 在棱
在棱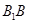 上,且满足
上,且满足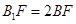 .
.
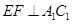 ;
;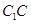 上确定一点
上确定一点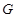 ,使
,使 、
、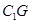 的长;
的长; 的体积.
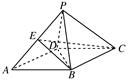
的体积.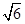 .
.
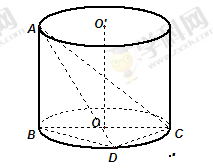
 是圆柱体
是圆柱体 的一条母线,
的一条母线,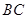 过底面圆的圆心
过底面圆的圆心 ,
,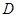 是圆
是圆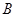 、
、 重合的任意一点,已知棱
重合的任意一点,已知棱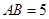 ,
,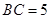 ,
,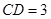 .
.
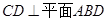 ;
;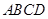 绕母线
绕母线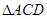 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.