题目内容
18.定义取整函数[x],它表示x的整数部分,即[x]是不超过x的最大整数,例如[2]=2,[3.1]=3,[-2.6]=-3等,设函数f(x)=$\frac{{2016}^{x}}{1{+2016}^{x}}$,x>0,则函数g(x)=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]的值域为{-1,0}.分析 令t(x)=$\frac{201{6}^{x}-1}{2(1+201{6}^{x})}$,判断其奇偶性,并求得t(x)=$\frac{1}{2}-\frac{1}{201{6}^{x}+1}$∈($-\frac{1}{2}$,$\frac{1}{2}$),然后分t(x)=0和t(x)≠0求解函数值域.
解答 解:∵f(x)=$\frac{201{6}^{x}}{1+201{6}^{x}}$,∴f(x)-$\frac{1}{2}$=$\frac{201{6}^{x}}{1+201{6}^{x}}$$-\frac{1}{2}$=$\frac{201{6}^{x}-1}{2(1+201{6}^{x})}$,
令t(x)=$\frac{201{6}^{x}-1}{2(1+201{6}^{x})}$,则t(-x)=$\frac{201{6}^{-x}-1}{2(1+201{6}^{-x})}=\frac{1-201{6}^{x}}{2(1+201{6}^{x})}$=-t(x),
即t(x)为奇函数,又t(x)=$\frac{1}{2}-\frac{1}{201{6}^{x}+1}$∈($-\frac{1}{2}$,$\frac{1}{2}$),
当t(x)=0时,[t(x)]+[t(-x)]=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]=0;
当t(x)≠0时,不妨设t(x)>0,则[t(x)]=0,[t(-x)]=-1,
则[t(x)]+[t(-x)]=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]=-1.
∴函数g(x)=[f(x)-$\frac{1}{2}$]+[f(-x)-$\frac{1}{2}$]的值域为{-1,0}.
故答案为:{-1,0}.
点评 本题考查函数值域的求法,考查函数奇偶性的性质,考查逻辑思维能力和推理运算能力,是中档题.

| 身高x(cm) | 160 | 165 | 170 | 175 | 180 |
| 体重y(kg) | 66 | 67 | 70 | 73 | 74 |
| A. | 70.9kg | B. | 71.2kg | C. | 70.55kg | D. | 71.05kg |
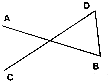
| A. | $\overrightarrow{AB}$-$\overrightarrow{CD}$ | B. | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{CD}$ | C. | $\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{CD}$) | D. | -($\overrightarrow{AB}$-$\overrightarrow{CD}$) |
| A. | 有最大值 | B. | 有最小值 | ||
| C. | 既无最大值又无最小值 | D. | 不确定 |
| A. | ∅?P?M | B. | M?P?I | C. | M=∅ | D. | P=I且M≠P |