题目内容
14.若集合A={1,m,m2},集合B={2,4},则“m=-2”是“A∩B={4}”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合集合的基本运算关系,进行判断即可.
解答 解:若A∩B={4},则m=4或m2=4,即m=4或m=2或m=-2,
当m=2时,集合A={1,2,4},A∩B={2,4}不成立,故m=4或m=-2,
即“m=-2”是“A∩B={4}”的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,根据集合的基本关系是解决本题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
4.已知抛物线C:y2=8x的焦点为F,点M(-1,0),不垂直于x轴的直线于抛物线相交于A,B两点,若x轴平分∠AMB,则△FAB的面积的取值范围是( )
| A. | (2$\sqrt{2}$,+∞) | B. | [2$\sqrt{2}$,+∞) | C. | (4$\sqrt{2}$,+∞) | D. | [4$\sqrt{2}$,+∞) |
5.已知点A是半径为1的⊙O外一点,且AO=2,若M,N是⊙O一条直径的两个端点,则$\overrightarrow{AM}$$•\overrightarrow{AN}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.设复数z1=1+i,z2=x+2i(x∈R),若z1z2为纯虚数,则x=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
3.定义在R上的奇函数f(x)和定义在{x|x≠0}上的偶函数g(x)分别满足f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(0≤x<1)}\\{\frac{1}{x}(x≥1)}\end{array}\right.$,g(x)=log2x(x>0),若存在实数a,使得f(a)=g(b)成立,则实数b的取值范围是( )
| A. | [-2,2] | B. | [-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$] | C. | [-2,-$\frac{1}{2}$]∪[$\frac{1}{2}$,2] | D. | (-∞,-2]∪[2,+∞) |
4.设A={x|y=$\sqrt{2x-1}$,x∈R},B={x|x2-3x-18<0},则A∩B=( )
| A. | ($\frac{1}{2}$,6) | B. | ($\frac{1}{2}$,3) | C. | [$\frac{1}{2}$,6) | D. | [$\frac{1}{2}$,3) |
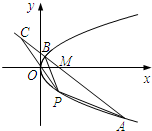 如图,在平面直角坐标系xOy中,点A(8,-4),P(2,t)(t<0)在抛物线y2=2px(p>0)上.
如图,在平面直角坐标系xOy中,点A(8,-4),P(2,t)(t<0)在抛物线y2=2px(p>0)上.