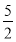题目内容
4.已知抛物线C:y2=8x的焦点为F,点M(-1,0),不垂直于x轴的直线于抛物线相交于A,B两点,若x轴平分∠AMB,则△FAB的面积的取值范围是( )| A. | (2$\sqrt{2}$,+∞) | B. | [2$\sqrt{2}$,+∞) | C. | (4$\sqrt{2}$,+∞) | D. | [4$\sqrt{2}$,+∞) |
分析 如图所示,设A(x1,y1),B(x2,y2).直线AB的方程为my=x+t(m≠0).与抛物线方程联立可得y2-8my+8t=0,得到根与系数的关系,由于x轴平分∠AMB,可得kMA+kMB=0,$\frac{{y}_{1}}{{x}_{1}+1}+\frac{{y}_{2}}{{x}_{2}+1}$=0,化为t=-1.利用弦长公式可得:|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,F(2,0)到直线AB的距离d=$\frac{1}{\sqrt{1+{m}^{2}}}$,再利用S△FAB=$\frac{1}{2}|AB|•d$及其二次函数的单调性即可得出.
解答 解:如图所示,
设A(x1,y1),B(x2,y2).直线AB的方程为my=x+t(m≠0).
联立$\left\{\begin{array}{l}{my=x+t}\\{{y}^{2}=8x}\end{array}\right.$,化为y2-8my+8t=0,
△>0,
∴y1+y2=8m,y1y2=8t,
∵x轴平分∠AMB,
∴kMA+kMB=0,
∴$\frac{{y}_{1}}{{x}_{1}+1}+\frac{{y}_{2}}{{x}_{2}+1}$=0,
∴y1(my2+1-t)+y2(my1+1-t)=0,
∴2my1y2+(1-t)(y1+y2)=0,
∴16mt+8m(1-t)=0,
化为t=-1.
∴|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\sqrt{(1+{m}^{2})(64{m}^{2}+32)}$=$4\sqrt{(1+{m}^{2})(4{m}^{2}+2)}$,
F(2,0)到直线AB的距离d=$\frac{|2-1|}{\sqrt{1+{m}^{2}}}$=$\frac{1}{\sqrt{1+{m}^{2}}}$,
∴S△FAB=$\frac{1}{2}|AB|•d$=$2\sqrt{4{m}^{2}+2}$$>2\sqrt{2}$.(m≠0).
∴△FAB的面积的取值范围是$(2\sqrt{2},+∞)$.
故选:A.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立可得根与系数的关系、角平分线的性质、斜率计算公式、弦长公式、三角形的面积计算公式、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 ,集合
,集合 ,则
,则 等于( )
等于( ) B.
B.
 D.
D.
 对任意
对任意 ,
, 满足
满足 ,且
,且 ,则
,则 等于( )
等于( ) B.
B.
 D.
D.
 是
是 所在平面内一点且
所在平面内一点且 ,现将一粒黄豆随机撕在
,现将一粒黄豆随机撕在 内的概率是( )
内的概率是( ) B.
B.
 D.
D.
 ,若向量
,若向量 与
与 平行,则
平行,则 ( )
( ) B.
B.
 D.
D.