题目内容
3.已知函数f(x)在(-1,1)上有定义,f($\frac{1}{2}$)=-1,且满足对于任意的x,y∈(-1,1),都有f(x)+f(y)=f($\frac{x+y}{1+xy}$),证明:f($\frac{4}{5}$)=-2.分析 利用赋值法,即可证明结论.
解答 证明:令x=y=$\frac{1}{2}$时,f($\frac{x+y}{1+xy}$)=f($\frac{1}{1+\frac{1}{4}}$)=f($\frac{4}{5}$).
∵对于任意的x,y∈(-1,1),都有f(x)+f(y)=f($\frac{x+y}{1+xy}$),
∴f($\frac{4}{5}$)=f($\frac{1}{2}$)+f($\frac{1}{2}$),
∵f($\frac{1}{2}$)=-1,
∴f($\frac{4}{5}$)=-2.
点评 本题考查求函数值,考查赋值法的运用,正确理解题意是关键.

练习册系列答案
相关题目
14.若函数f(x)在区间[-2,2]上的图象是一条连续不断的曲线,且函数f(x)在(-2,2)上仅有一个零点,则f(-2)•f(2)的符号是( )
| A. | 小于零 | B. | 大于零 | C. | 小于或大于零 | D. | 不能确定 |
11.已知集合P={α|2kπ≤α≤(2k+1)π,k∈Z},Q={α|-4≤α≤4},则P∩Q=( )
| A. | φ | B. | {α|-4≤α≤-π,或0≤α≤π} | ||
| C. | {α|-4≤α≤4} | D. | {α|0≤α≤π} |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别F1(-c,0),F2(c,0),若双曲线上存在点P,使得csin∠PF1F2=asin∠PF2F1,则该曲线的离心率的取值范围是( )
| A. | (1,$\sqrt{2}$] | B. | (1,$\sqrt{3}$] | C. | (1,$\sqrt{2}$+1] | D. | (1,$\sqrt{3}$+1] |
8.函数y=3x+log3(x+2)在[0,1]上的最大值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.若函数f(x)=2lgx-lg(x-1)-lga有两个零点,则a的取值范围是( )
| A. | 0≤a≤2 | B. | 2<a≤4 | C. | a≥4 | D. | a>4 |
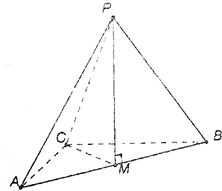 已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.
已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.