题目内容
过椭圆 的左顶点A做圆x2+y2=b2的切线,切点为B,延长AB交抛物线于y2=4ax于点C,若点B恰为A、C的中点,则
的左顶点A做圆x2+y2=b2的切线,切点为B,延长AB交抛物线于y2=4ax于点C,若点B恰为A、C的中点,则 的值为________.
的值为________.

分析:由抛物线于y2=4ax得到焦点F(a,0),连接OB,CF.由O,B分别是线段AF,AC的中点,可得|CF|=2|OB|=2b,利用抛物线的定义得xC+a=2b,得到xC=2b-a,进而得到点C的坐标,
由直线AC与圆x2+y2=b2的相切的性质即可得出.
解答:如图所示,

由抛物线于y2=4ax得到焦点F(a,0),连接OB,CF.
∵O,B分别是线段AF,AC的中点,∴|CF|=2|OB|=2b,
∴点C的横坐标满足xC+a=2b,得到xC=2b-a,
由
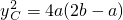 ,解得
,解得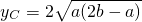 (取yC>0).
(取yC>0).∴C
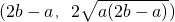 .
.∴直线AC的方程为
 ,化为
,化为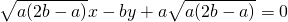 .
.∵直线AC与圆x2+y2=b2的相切,∴
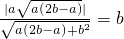 ,
,化为(a2-ab-b2)2=0,即a2-ab-b2=0,化为
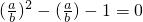 .又∵
.又∵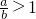 .
.解得
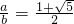 .
.故答案为
 .
.点评:熟练掌握圆锥曲线的定义、标准方程及性质、直线与圆相切的性质、点到直线的距离公式是解题的关键.本题需要较强的计算能力.

练习册系列答案
相关题目
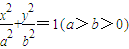 的左顶点A做圆x2+y2=b2的切线,切点为B,延长AB交抛物线于y2=4ax于点C,若点B恰为A、C的中点,则
的左顶点A做圆x2+y2=b2的切线,切点为B,延长AB交抛物线于y2=4ax于点C,若点B恰为A、C的中点,则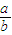 的值为 .
的值为 .