题目内容
14.某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨、160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,则该颜料公司一天之内可获得的最大利润为14000元.分析 设一天生产A产品x钝,B产品y钝,列出约束条件,作出平面区域,根据平面区域得出最优解位置,得出最大值.
解答 解:设该公司每天生产A产品x钝,生产B产品y钝,则一天的利润为z=300x+200y,
其中$\left\{\begin{array}{l}{x+y≤50}\\{4x≤160}\\{2x+5y≤200}\end{array}\right.$,
作出平面区域如图所示: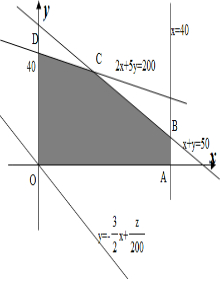
由z=300x+200y得y=-$\frac{3}{2}x$+$\frac{z}{200}$,
由图象可知直线y=-$\frac{3}{2}x$+$\frac{z}{200}$经过点B时,直线截距最大,此时z最大.
解方程组$\left\{\begin{array}{l}{x=40}\\{x+y=50}\end{array}\right.$得$\left\{\begin{array}{l}{x=40}\\{y=10}\end{array}\right.$,
∴z的最大值为300×40+200×10=14000.
故答案为:14000元.
点评 本题考查了简单的线性规划的应用,属于中档题.

练习册系列答案
相关题目
4. 如果如图所示程序执行后输出的结果是480,那么在程序UNTIL后面的“条件”应为( )
如果如图所示程序执行后输出的结果是480,那么在程序UNTIL后面的“条件”应为( )
 如果如图所示程序执行后输出的结果是480,那么在程序UNTIL后面的“条件”应为( )
如果如图所示程序执行后输出的结果是480,那么在程序UNTIL后面的“条件”应为( )| A. | i>8 | B. | i>=8 | C. | i<8 | D. | i<=8 |
5.已知点P在曲线y=$\frac{4}{{{e^x}+1}}$上,θ为曲线在点P处的切线的倾斜角,则θ的取值范围是( )
| A. | [0,$\frac{π}{4}$) | B. | $[\frac{π}{4},\frac{π}{2})$ | C. | $[\frac{3π}{4},π)$ | D. | $(\frac{π}{2},\frac{3π}{4}]$ |
2.过抛物线C:y2=4x的焦点F的直线交抛物线C于A,B两点,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x轴交于点M,则M的横坐标的取值范围为( )
| A. | (-∞,0) | B. | (0,2) | C. | (2,+∞) | D. | (-∞,0)∪(2,+∞) |
3.二项式${(2x-\frac{1}{x})^5}$展开式中,第四项的系数为( )
| A. | 40 | B. | -40 | C. | 80 | D. | -80 |