题目内容
已知一焦点在x轴上,中心在原点的双曲线的实轴等于虚轴,且图象经过点
.
(1)求该双曲线的方程;
(2)若直线y=kx+1与该双曲线只有一个公共点,求实数k的值.
|
(1)求该双曲线的方程;
(2)若直线y=kx+1与该双曲线只有一个公共点,求实数k的值.
(1)∵a=b,∴所求圆锥曲线为等轴双曲线.
∴设双曲线方程为
-
=1
,
∵图象经过点
,∴
-
=1,解得a=1,
∴所求双曲线方程为x2-y2=1;
(2)由
?(k2-1)x2+2kx+2=0,
,
∴k=-1、1、
、-
,直线与双曲线有一个公共点.
∴设双曲线方程为
| x2 | ||||
|
| y2 | ||||
|
|
∵图象经过点
|
| 22 | ||||
|
| ||||||
|
∴所求双曲线方程为x2-y2=1;
(2)由
|
|
|
∴k=-1、1、
| 2 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率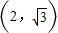 .
.