题目内容
设函数 .
.
(I )讨论f(x)的单调性;
(II) ( i )若证明:当x>6 时,
(ii)若方程f(x)=a有3个不同的实数解,求a的取值范围.
【答案】
(Ⅰ)f¢(x)=-e-x[x2-(a+2)x+2a]=-e-x(x-2)(x-a). …1分
(1)若a=2,则f¢(x)≤0,f(x)在(-∞,+∞)单调递减. …2分
(2)若0≤a<2,当x变化时,f¢(x)、f(x)的变化如下表:
|
x |
(-∞,a) |
a |
(a,2) |
2 |
(2,+∞) |
|
f¢(x) |
- |
0 |
+ |
0 |
- |
|
f(x) |
↘ |
极小值ae-a |
↗ |
极大值(4-a)e-2 |
↘ |
此时f(x)在(-∞,a)和(2,+∞)单调递减,在(a,2)单调递增. …3分
(3)若a>2,当x变化时,f¢(x)、f(x)的变化如下表:
|
x |
(-∞,2) |
2 |
(2,a) |
a |
(a,+∞) |
|
f¢(x) |
- |
0 |
+ |
0 |
- |
|
f(x) |
↘ |
极小值(4-a)e-2 |
↗ |
极大值ae-a |
↘ |
此时f(x)在(-∞,2)和(a,+∞)单调递减,在(2,a)单调递增. …4分
(Ⅱ)(ⅰ)若a=0,则f(x)=x2e-x,f(x)< 即x3<ex.
即x3<ex.
当x>6时,所证不等式等价于x>3lnx,
设g(x)=x-3lnx,当x>6时,g¢(x)=1- >0,g(x)单调递增,
>0,g(x)单调递增,
有g(x)>g(6)=3(2-ln6)>0,即x>3lnx.
故当x>6时,f(x)< . …6分
. …6分
(ⅱ)根据(Ⅰ),
(1)若a=2,方程f(x)=a不可能有3个不同的实数解. …7分

【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的单调性;
的单调性; 和
和 ,记过点
,记过点 的直线的斜率为
的直线的斜率为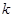 ,问:是否存在
,问:是否存在 ,使得
,使得 ?若存在,求出
?若存在,求出
 的单调性;
的单调性; 和
和 ,记过点
,记过点 的直线的斜率为
的直线的斜率为 ,问:是否存在
,问:是否存在 ,使得
,使得 ?若存在,求出
?若存在,求出
 的单调性;
的单调性; ,记过点
,记过点 的直线的斜率为
的直线的斜率为 ,问:是否存在
,问:是否存在 ,使得
,使得 若存在,求出
若存在,求出