题目内容
18.已知某圆锥曲线和椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1有相同的焦点,且经过圆(x-4)2+(y+$\sqrt{15}$)2=64的圆心,求此圆锥曲线的方程.分析 由已知椭圆方程求出椭圆的焦点坐标,求出圆的圆心坐标,然后分所求曲线是椭圆和双曲线讨论,利用定义求出椭圆的长半轴和双曲线的实半轴,再由隐含条件求出对应的短半轴和虚半轴,则圆锥曲线方程可求.
解答 解:由椭圆方程$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,得${{a}_{1}}^{2}=25,{{b}_{1}}^{2}=16$,∴${c}^{2}={{a}_{1}}^{2}-{{b}_{1}}^{2}=9$.
∴椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点坐标为F1(-3,0),F2(3,0).
又圆(x-4)2+(y+$\sqrt{15}$)2=64的圆心坐标为(4,-$\sqrt{15}$),
若所求圆锥曲线为椭圆,则2a=$\sqrt{(4+3)^{2}+(-\sqrt{15})^{2}}+\sqrt{(4-3)^{2}+(-\sqrt{15})^{2}}$=12.
∴a=6,则b2=a2-c2=36-9=27.
椭圆方程为:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}=1$;
若所求圆锥曲线为双曲线,则2a=$\sqrt{(4+3)^{2}+(-\sqrt{15})^{2}}-\sqrt{(4-3)^{2}+(-\sqrt{15})^{2}}$=4.
∴a=2,则b2=c2-a2=9-4=5.
双曲线方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}=1$.
点评 本题是圆与圆锥曲线的综合题,考查了椭圆、双曲线的定义,考查了椭圆与双曲线的几何性质,是中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
8.定义在R的奇函数f(x),当x<0时,f(x)=-x2+x,则x>0时,f(x)等于( )
| A. | x2+x | B. | -x2+x | C. | -x2-x | D. | x2-x |
9.函数y=log2x+3的值域是( )
| A. | [2,+∞) | B. | (3,+∞) | C. | [3,+∞) | D. | (-∞,+∞) |
7.p:x2-3x+2≤0成立的一个必要不充分条件是( )
| A. | x>1 | B. | x≥1 | C. | 1≤x≤2 | D. | 1<x<2 |
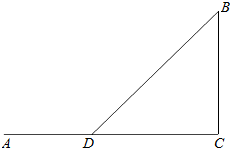 如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.
如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.