题目内容

已知f(x)=()2(x≥1),

(1)求f(x)的反函数f-1(x),并求出反函数的定义域;

(2)判断并证明f-1(x)的单调性.

解：(1)设y=()2x=,又x≥1,

∴≥10≤y＜1,即f-1(x)=,f-1(x)的定义域为［0,1］.

(2)f-1(x)在［0,1)上单调递增.

证明如下:设0≤x1＜x2＜1,∴0≤＜＜1.

∴f-1(x1)-f-1(x2)=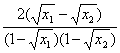＜0.∴f-1(x)在［0,1］上单调递增.

练习册系列答案
相关题目
已知f(x)=
(2-a)x+1(x＜1)
ax(x≥1)
满足对任意x1≠x2，都有
f(x1)-f(x2)
x1-x2
＞0成立，那么a的取值范围是（　　）
已知f(x)=
2-
x+3
x+1
的定义域为A，集合B={x|2a≤x≤a+1}
（1）求集合A
（2）若B⊆A，求实数a的取值范围．
（2007•惠州模拟）设n为正整数，规定：fn(x)=
f{f[…f(x)]}
n个f
，已知f(x)=
2(1-x)，0≤x≤1
x-1，1＜x≤2
，
（1）解不等式f（x）≤x；
（2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
（3）求f2007(
8
9
)的值；
（4）若集合B={x|f12（x）=x，x∈[0，2]}，证明：B中至少包含8个元素．
已知f(x)=2+x2cos(
π
2
+x)在[-a，a](a＞0)上的最大值与最小值分别为M、m，则M+m的值为（　　）
已知n为正整数，规定f1（x）=f（x），fn+1（x）=f（fn（x）），已知f(x)=
2(1-x)，0≤x≤1
x-1，
 1＜x≤2
，
（1）解不等式f（x）≤x；
（2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网