题目内容
12．已知f（x）=algx+1-a对任意a∈[-1，1]恒有f（x）＞0，则x的取值范围是（ ）| A． | （0，100） | B． | （1，100） | C． | （0，10） | D． | （10，100） |
分析 令g（a）=a（lgx-1）+1，由题意可得$\left\{\begin{array}{l}{g（-1）＞0}\\{g（1）＞0}\end{array}\right.$，由对数不等式的解法，即可得到所求范围．
解答 解：令g（a）=a（lgx-1）+1，
由题意可得$\left\{\begin{array}{l}{g（-1）＞0}\\{g（1）＞0}\end{array}\right.$，
即为$\left\{\begin{array}{l}{-（lgx-1）+1＞0}\\{lgx-1+1＞0}\end{array}\right.$，
即有$\left\{\begin{array}{l}{0＜x＜100}\\{x＞10}\end{array}\right.$，
解得10＜x＜100．
故选：D．
点评 本题考查函数的单调性的运用：解不等式，注意构造一次函数，运用一次函数的单调性，考查运算能力，属于中档题．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
7．当a＞0且a≠1时，把函数y=a-x和y=logax的图象画在同一平面直角坐标系中，可以是（ ）
| A． | ①② | B． | ①③ | C． | ②③ | D． | ③④ |
1．已知函数f（x）的定义域为（0，+∞），若y=$\frac{f（x）}{x}$在（0，+∞）上为增函数，则称f（x）为“一阶比增函数”；若y=$\frac{f（x）}{{x}^{2}}$在（0，+∞）上为增函数，则称f（x）为“二阶比增函数”．我们把所有“一阶比增函数”组成的集合记为Ω1，所有“二阶比增函数”组成的集合记为Ω2，．
（Ⅰ）已知函数f（x）=x3-2hx2-hx，若f（x）∈Ω1，且f（x）∉Ω2，求实数h的取值范围；
（Ⅱ）已知0＜a＜b＜c，f（x）∈Ω1且f（x）的部分函数值由下表给出，
求证：d（2d+t-4）＞0；
（Ⅲ）定义集合Ψ={f（x）|f（x）∈Ω2}，且存在常数k，使得任取x∈（0，+∞），f（x）＜k}，请问：是否存在常数m，使得?f（x）∈Ψ，?x∈（0，+∞），有f（x）＜M成立？若存在，求出M的最小值；若不存在，说明理由．
（Ⅰ）已知函数f（x）=x3-2hx2-hx，若f（x）∈Ω1，且f（x）∉Ω2，求实数h的取值范围；
（Ⅱ）已知0＜a＜b＜c，f（x）∈Ω1且f（x）的部分函数值由下表给出，
| x | a | b | c | a+b+c |
| f（x） | d | d | t | 4 |
（Ⅲ）定义集合Ψ={f（x）|f（x）∈Ω2}，且存在常数k，使得任取x∈（0，+∞），f（x）＜k}，请问：是否存在常数m，使得?f（x）∈Ψ，?x∈（0，+∞），有f（x）＜M成立？若存在，求出M的最小值；若不存在，说明理由．
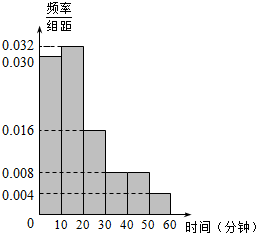某校决定为本校上学时间不少于30分钟的学生提供校车接送服务．为了解学生上学所需时间，从全校600名学生中抽取50人统计上学时间（单位：分钟），现对600人随机编号为001，002，…600．抽取50位学生上学时间均不超过60分钟，将时间按如下方式分成六组，第一组上学时间在[0，10），第二组上学时间在[10，20），…第六组上学时间在[50，60]得到各组人数的频率分布直方图．如图．