题目内容
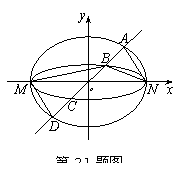
如图,已知椭圆![]() 与
与![]() 的中心在坐标原点
的中心在坐标原点![]() ,长轴均为
,长轴均为![]() 且在
且在![]() 轴上,短轴长分别为
轴上,短轴长分别为![]() ,
,![]()
![]() ,过原点且不与
,过原点且不与![]() 轴重合的直线
轴重合的直线![]() 与
与![]() ,
,![]() 的四个交点按纵坐标从大到小依次为
的四个交点按纵坐标从大到小依次为![]() ,
,![]() ,
,![]() ,
,![]() 。记
。记![]() ,
,![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() 。
。
(I)当直线![]() 与
与![]() 轴重合时,若
轴重合时,若![]() ,求
,求![]() 的值;
的值;
(II)当![]() 变化时,是否存在与坐标轴不重合的直线
变化时,是否存在与坐标轴不重合的直线![]() ,使得
,使得![]() ?并说明理由。
?并说明理由。
【解析与答案】(I)![]()
![]() ,
,
解得:![]() (舍去小于1的根)
(舍去小于1的根)
(II)设椭圆![]() ,
,![]() ,直线
,直线![]() :
:![]()

![]()
![]()
同理可得,![]()
又![]()
![]() 和
和![]() 的的高相等
的的高相等
![]()
如果存在非零实数![]() 使得
使得![]() ,则有
,则有![]() ,
,
即:![]() ,解得
,解得![]()
![]() 当
当![]() 时,
时,![]() ,存在这样的直线
,存在这样的直线![]() ;当
;当![]() 时,
时,![]() ,不存在这样的直线
,不存在这样的直线![]() 。
。
【相关知识点】直线与椭圆相交的问题(计算异常复杂)

练习册系列答案
相关题目
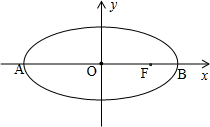 在平面直角坐标系xoy中,如图,已知椭圆
在平面直角坐标系xoy中,如图,已知椭圆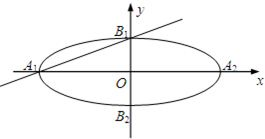
 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: (2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0
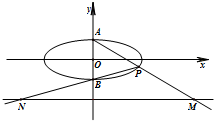
(2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0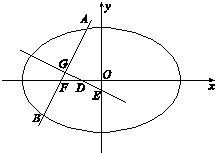 (2013•甘肃三模)如图,已知椭圆
(2013•甘肃三模)如图,已知椭圆