题目内容
线段AB过点M(m,0)(m>0),如图,并且点A、B到x轴的距离之积为4 m,抛物线C以x轴为对称轴且经过O、A、B三点.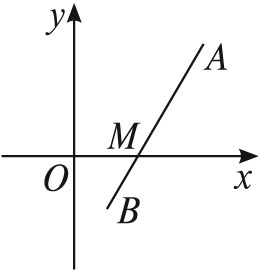
(1)求抛物线C的方程;
(2)当m=1,|AM|=2|MB|时,求直线AB的方程.
解:(1)由题可设抛物线的方程为y2=2px(p>0).
当线段AB垂直于x轴时,A、B的坐标为(m,±2![]() ),
),
∴(2![]() )2=2p·m.
)2=2p·m.
∴2p=4.
当线段AB与x轴不垂直时,设直线AB的斜率为k(k≠0),则直线AB的方程为y=k(x-m).
由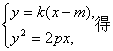
y2-![]() y-2pm=0.
y-2pm=0.
∴A、B两点的纵坐标的积为-2pm.
由题知|-2pm|=4m,
∴2p=4.
综上所述,抛物线C的方程为y2=4x.
(2)设A(x1,y1)、B(y2,y2),
由(1)可得y2-![]() y-4=0,
y-4=0,
∴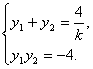
∵M的纵坐标为0,|AM|=2|MB|,
∴![]() ,即y1=-2y2.
,即y1=-2y2.
把y1=-2y2代入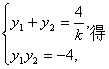
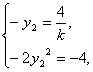 消去y2得k=±2
消去y2得k=±2![]() ,
,
∴直线AB的方程为y=±2![]() (x-1).
(x-1).
绿色通道:
当设直线的点斜式方程时,应首先考虑直线的斜率是否存在.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
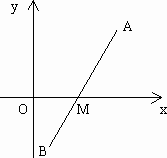
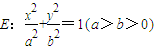 的右顶点和上顶点,过原点O作直线交线段AB于点M(异于点A,B),交椭圆于C,D两点(点C在第一象限内),△ABC和△ABD的面积分别为S1与S2.
的右顶点和上顶点,过原点O作直线交线段AB于点M(异于点A,B),交椭圆于C,D两点(点C在第一象限内),△ABC和△ABD的面积分别为S1与S2.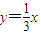 ,求椭圆的离心率;
,求椭圆的离心率;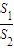 的最大值.
的最大值.