Question

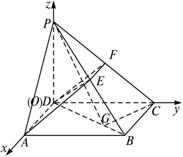
已知ABCD为矩形,PD⊥平面ABCD,PD=DC=23,AD=2,E为PB上一点,且PC⊥平面ADE.

(1)求PC与平面PBD所成角的大小;

(2)求的值;

(3)求四棱锥P—ABCD夹在平面ADE与底面ABCD之间部分的体积.

Answer 1

(1)解:在平面ABCD内作CG⊥BD于G,连PG,

∵PD⊥平面ABCD,CG平面ABCD,

∴PD⊥CG.

∴CG⊥面PBD.

∴∠CPG就是PC与面PBD所成的角.                                        

在Rt△BCD中,CG==,又PC=2,

故在Rt△PGC中,sin∠CPG==.

又∵∠CPG为锐角,∴∠CPG=arcsin.

∴PC与面PBD所成的角为arcsin.                                      

(2)解法一:设平面ADE与PC交于点F,连DF、EF,

∵PC⊥面ADE,DF平面ADE,

∴PC⊥DF.

又∵PD=DC,∴F为PC的中点.                                            

∵BC∥AD,BC平面ADE,

∴BC∥平面ADE.

又平面ADE∩平面PBC=EF,

∴BC∥EF.

∴E为PB的中点,故=1.                                               

解法二:建立如图的空间直角坐标系O—xyz,则D(0,0,0),A(2,0,0),B(2,,0),C(0, ,0),P(0,0,),

=(2,,), =(0,,).

设=λ,则=λ=(2λ,λ,λ),

∴=+=(2λ, λ,-λ).                            

由PC⊥平面ADE,可知PC⊥DE,

∴·=0,即12λ-12(1-λ)=0,解得λ=,即PE=PB.

∴=1.                                                                 

(3)解:∵PD⊥平面ABCD,∴PD⊥AD.

又AD⊥DC,∴AD⊥平面PDC.

又DF平面PDC,∴AD⊥DF.

∵EF∥BC,BC∥AD,∴EF∥AD.

又PF⊥平面ADEF,EF=BC=1,DF=DC=,                              

∴V_P—DAEF=××=3.

又V_P—ABCD=×(2×)×=8,

∴V=V_P—ABCD-V_P—DAEF=5,

即四棱锥P—ABCD夹在平面ADE与底面ABCD之间部分的体积为5.