题目内容
已知过抛物线y2=4x的焦点F的弦长为36,求弦所在的直线方程.
思路分析:弦所在的直线经过焦点(1,0),只需求出直线的斜率,因为弦长为36,所以可以判断直线的斜率是存在的且不为0.
解析:由题意可设弦所在的直线的斜率为k,且与抛物线交于A(x1,y1)、B(x2,y2)两点.
∵抛物线y2=4x的焦点F(1,0),
∴直线方程为y=k(x-1).
由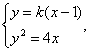
整理得k2x2-(2k2+4)x+k2=0.
∴x1+x2=![]() .
.
∴|AB|=|AF|+|BF|
=x1+x2+2=![]() +2.
+2.
又|AB|=36,∴![]() +2=36,
+2=36,
解得k2=![]() ,即k=±
,即k=±![]() .
.
∴所求直线方程为y=![]() (x-1)或y=-
(x-1)或y=-![]() (x-1).
(x-1).
温馨提示
(1)此题也可以先求出两交点坐标,再根据两点间的距离公式列出等式求出k,但是计算复杂,一般不采用.
(2)也可以利用弦长公式|AB|=![]() |x1-x2|来求,这个方法普遍适用于求二次曲线的弦长.
|x1-x2|来求,这个方法普遍适用于求二次曲线的弦长.
(3)因为本题的弦是过焦点的,是特殊位置的弦,所以结合抛物线的定义得到|AB|=x1+x2+p,解起来更简捷.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
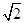 ,则m6+ m4的值为( )
,则m6+ m4的值为( )