题目内容
已知过抛物线y2=4x焦点F的直线l与抛物线相交于A,B两点,若|AF|=4,则|BF|= .
分析:根据抛物线方程可求得焦点坐标和准线方程,设过F的直线方程,与抛物线方程联立,整理后,设A(x1,y1),B(x2,y2)根据韦达定理可求得x1x2的值,又根据抛物线定义可知|AF|=x1+1,|BF|=x2+1代入
+
可得其值为1,再由|AF|=4,即可得到|BF|.
| 1 |
| |AF| |
| 1 |
| |BF| |
解答:解:易知F坐标(1,0)准线方程为x=-1.
设过F点直线方程为y=k(x-1)
代入抛物线方程,得 k2(x-1)2=4x.
化简后为:k2x2-(2k2+4)x+k2=0.
设A(x1,y1),B(x2,y2)
则有x1x2=1
根据抛物线性质可知,|AF|=x1+1,|BF|=x2+1
∴
+
=
=
=
=1,
又由|AF|=4,则|BF|=
=
.
故答案为:
.
设过F点直线方程为y=k(x-1)
代入抛物线方程,得 k2(x-1)2=4x.
化简后为:k2x2-(2k2+4)x+k2=0.
设A(x1,y1),B(x2,y2)
则有x1x2=1
根据抛物线性质可知,|AF|=x1+1,|BF|=x2+1
∴
| 1 |
| |AF| |
| 1 |
| |BF| |
| x1+1+x2+1 |
| (x1+1)(x2+1) |
| x1+x2+2 |
| x1+x2+x1x2+1 |
| x1+x2+2 |
| x1+x2+2 |
又由|AF|=4,则|BF|=
| 1 | ||
1-
|
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题主要考查抛物线的应用和抛物线定义.对于过抛物线焦点的直线与抛物线关系,常用抛物线的定义来解决.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
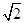 ,则m6+ m4的值为( )
,则m6+ m4的值为( )