题目内容
已知点A(λ+1,μ-1,3),B(2λ,μ,λ-2μ),C(λ+3,μ-3,9)三点共线,则λ=
0
0
,μ=0
0
.分析:根据所给的三个点的坐标,写出两个向量 的坐标,根据三个点共线,得到两个向量之间的共线关系,得到两个向量之间的关系,即一个向量的坐标等于实数倍的另一个向量的坐标,写出关系式,得到λ,μ即可.
解答:解:∵A(λ+1,μ-1,3),B(2λ,μ,λ-2μ),C(λ+3,μ-3,9)
∴
=(λ-1,1,λ-2μ-3),
=(2,-2,6)
∵A,B,C三点共线,
∴
=k
,
∴(λ-1,1,λ-2μ-3)=k(2,-2,6)
∴
∴k=-
,λ=0,μ=0.
故答案为:0;0.
∴
| AB |
| AC |
∵A,B,C三点共线,
∴
| AB |
| AC |
∴(λ-1,1,λ-2μ-3)=k(2,-2,6)
∴
|
| 1 |
| 2 |
故答案为:0;0.
点评:本题考查向量共线,考查三点共线与两个向量共线的关系,考查向量的坐标之间的运算,是一个基础题.

练习册系列答案
相关题目
已知点A(1,-1)及圆 x2+y2-4x+4y+4=0,则过点A,且在圆上截得的弦为最长的弦所在的直线方程是( )
| A、x-1=0 | B、x+y=0 | C、y+1=0 | D、x-y-2=0 |
已知点A(1,0),直线l:y=2x-4,点R是直线l上的一点.若
=
,则点P的轨迹方程为( )
| RA |
| AP |
| A、y=-2x |
| B、y=2x |
| C、y=2x-8 |
| D、y=2x+4 |
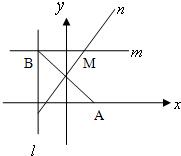 已知点A(1,0),定直线l:x=-1,B为l上的一个动点,过B作直线m⊥l,连接AB,作线段AB的垂直平分线n,交直线m于点M.
已知点A(1,0),定直线l:x=-1,B为l上的一个动点,过B作直线m⊥l,连接AB,作线段AB的垂直平分线n,交直线m于点M.