题目内容
过点(1,0)且倾斜角是直线2x+3y+3=0的倾斜角的两倍的直线方程是 .
【答案】分析:先求直线2x+3y+3=0的斜率,进而转化为倾斜角,用二倍角公式求过点(1,0)的斜率,再求解直线方程.
解答:解:直线2x+3y+3=0的斜率为k=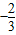 ,倾斜角为α,所以tanα=
,倾斜角为α,所以tanα=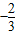 ,
,
过点(1,0)的倾斜角为2α,其斜率为tan2α=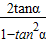 =
=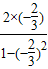 =
=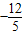 ,
,
故所求直线方程为:y=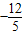 (x-1),即12x+5y-12=0
(x-1),即12x+5y-12=0
故答案为:12x+5y-12=0.
点评:本题关键是倾斜角的二倍和斜率的关系互化,考查计算能力.
解答:解:直线2x+3y+3=0的斜率为k=
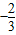 ,倾斜角为α,所以tanα=
,倾斜角为α,所以tanα=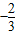 ,
,过点(1,0)的倾斜角为2α,其斜率为tan2α=
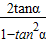 =
=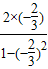 =
=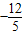 ,
,故所求直线方程为:y=
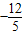 (x-1),即12x+5y-12=0
(x-1),即12x+5y-12=0故答案为:12x+5y-12=0.
点评:本题关键是倾斜角的二倍和斜率的关系互化,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目