题目内容
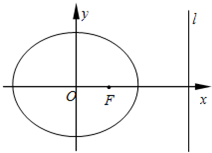 如图,F是中心在原点、焦点在x轴上的椭圆C的右焦点,\直线l:x=4是椭圆C的右准线,F到直线l的距离等于3.
如图,F是中心在原点、焦点在x轴上的椭圆C的右焦点,\直线l:x=4是椭圆C的右准线,F到直线l的距离等于3.(1)求椭圆C的方程;
(2)点P是椭圆C上动点,PM⊥l,垂足为M.是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
分析:(1)设椭圆C的方程为
+
=1(a>b>0),由已知,得出a,b的方程,解得a,b.最后写出椭圆C的方程即可;
(2)由
=e=
,得PF=
PM.∴PF≠PM.下面分类讨论:①若PF=FM,②若FM=PM,结合已知条件求得第②情形存在点P(
,±
),使得△PFM为等腰三角形.
| x2 |
| a2 |
| y2 |
| b2 |
(2)由
| PF |
| PM |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 7 |
3
| ||
| 7 |
解答:解:(1)设椭圆C的方程为
+
=1(a>b>0),
由已知,得
∴
∴b=
.
所以椭圆C的方程为
+
=1.
(2)由
=e=
,得PF=
PM.∴PF≠PM.
①若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,∴PF不可能与PM相等.
②若FM=PM,设P(x,y)(x≠±2),则M(4,y).
∴
=4-x,∴9+y2=16-8x+x2,又由
+
=1,得y2=3-
x2.
∴9+3-
x2=16-8x+x2,∴
x2-8x+4=0.∴7x2-32x+16=0.
∴x=
或x=4.∵x∈(-2,2),∴x=
.∴P(
,±
).
综上,存在点P(
,±
),使得△PFM为等腰三角形.
| x2 |
| a2 |
| y2 |
| b2 |
由已知,得
|
|
| 3 |
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由
| PF |
| PM |
| 1 |
| 2 |
| 1 |
| 2 |
①若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,∴PF不可能与PM相等.
②若FM=PM,设P(x,y)(x≠±2),则M(4,y).
∴
| 32+y2 |
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 4 |
∴9+3-
| 3 |
| 4 |
| 7 |
| 4 |
∴x=
| 4 |
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
3
| ||
| 7 |
综上,存在点P(
| 4 |
| 7 |
3
| ||
| 7 |
点评:本题考查椭圆的性质和应用,解题的关键是要认真审题,仔细解答,注意合理地选用反证法的思想方法证题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
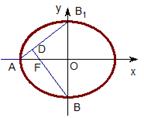
 如图,椭圆的中心在原点,F为椭圆的左焦点,B为椭圆的一个顶点,过点B作与FB垂直的直线BP交x轴于P点,且椭圆的长半轴长a和短半轴长b是关于x的方程
如图,椭圆的中心在原点,F为椭圆的左焦点,B为椭圆的一个顶点,过点B作与FB垂直的直线BP交x轴于P点,且椭圆的长半轴长a和短半轴长b是关于x的方程 cx+2c2=0(其中c为半焦距)的两个根。
cx+2c2=0(其中c为半焦距)的两个根。
 相切,试求椭圆的方程。
相切,试求椭圆的方程。 (其中c为半焦距)的两个根.
(其中c为半焦距)的两个根. 相切,试求椭圆的方程.
相切,试求椭圆的方程.
 A
A