题目内容

函数f(x)(x∈R)由x-lnf(x)=0确定，则导函数y=f′(x)图象的大致形状是（    ）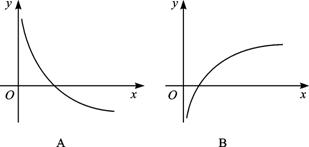

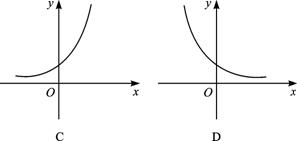
解析：由x-lnf(x)=0得lnf(x)=x=lnex,

∴f(x)=ex.

∴f′(x)=ex为指数函数，e＞1.

∴选C.

答案:C

练习册系列答案
相关题目
下面对命题“函数f（x）=x+
1
x
是奇函数”的证明不是综合法的是（　　）
设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
①f(-
3
4
) ＜f(
15
2
)；
②当x∈[-1，0]时f（x）=x3+4x+3；
③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
其中真命题的个数为（　　）
已知函数f（x）=x2-2ax+2a2-2（a≠0），g（x）=-ex-
1
ex
，则下列命题为真命题的是（　　）
A、?x∈R，都有f（x）＜g（x）
B、?x∈R，都有f（x）＞g（x）
C、?x0∈R，使得f（x0）＜g（x0）
D、?x0∈R，使得f（x0）=g（x0）

若函数f(x)和g(x)的定义域、值域都是R，则不等式f(x)> g(x)有解的充要条件是（　　）

A．$ x∈R, f(x)>g(x)                        B．有无穷多个x (x∈R )，使得f(x)>g(x)

C．" x∈R,f(x)>g(x)                         D．{ x∈R| f(x)≤g(x)}=F

 
下面对命题“函数f（x）=x+
1
x
是奇函数”的证明不是综合法的是（　　）
A．?x∈R且x≠0有f（-x）=（-x）+
1
-x
=-（x+
1
x
）=-f（x），∴f（x）是奇函数
B．?x∈R且x≠0有f（x）+f（-x）=x+
1
x
+（-x）+（-
1
x
）=0，∴f（x）=-f（-x），∴f（x）是奇函数
C．?x∈R且x≠0，∵f（x）≠0，∴
f(-x)
f(x)
=
-x-
1
x
x+
1
x
=-1，∴f（-x）=-f（x），∴f（x）是奇函数
D．取x=-1，f（-1）=-1+
1
-1
=-2，又f（1）=1+
1
1
=2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网