题目内容
点P是△ABC所在平面内的一点,且满足 ,则△PAC的面积与△ABC的面积之比为( )
,则△PAC的面积与△ABC的面积之比为( )
A. | B. | C. | D. |
C
解析试题分析:由于 ,所以
,所以 即
即 ,而
,而 ,
, ,答案选C.
,答案选C.
考点:向量的运算与三角形的面积公式

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
如图,已知在?ABCD中,O1,O2,O3为对角线BD上三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于F,则AD∶FD等于( )
| A.19∶2 | B.9∶1 |
| C.8∶1 | D.7∶1 |
如图所示,PC与圆O相切于点C,直线PO交圆O于A,B两点,弦CD垂直AB于E,则下面结论中,错误的结论是( )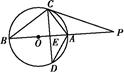
| A.△BEC∽△DEA |
| B.∠ACE=∠ACP |
| C.DE2=OE·EP |
| D.PC2=PA·AB |
如图,在矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△PBA,△APD,△CDP两两相似,则a,b间的关系一定满足( )
A.a≥ b b | B.a≥b | C.a≥ b b | D.a≥2b |
如图所示,已知O是圆心,直径AB和弦CD相交于点P,PA=2,PC=6,PD=4,则AB等于
| A.3 | B.8 | C.12 | D.14 |
若 =
= ,则下列各式一定成立的是
,则下列各式一定成立的是
A.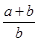 = =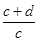 | B.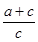 = = |
C. = = | D.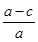 = = |
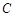 经过点
经过点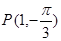 ,圆心为直线
,圆心为直线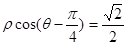 与极轴的交点,求圆
与极轴的交点,求圆 ,
, 、
、 分别是
分别是 两边上的动点。
两边上的动点。 ,
, 时,求
时,求 的长;
的长; 、
、 长度之和为定值4,求线段
长度之和为定值4,求线段
 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
(
 为参
为参 数).
数). 坐标方程化为直角坐标方程;
坐标方程化为直角坐标方程; 线
线 、
、 两点,求
两点,求 长.
长.