题目内容
【题目】已知函数![]() 定义在
定义在![]() 上的奇函数,
上的奇函数, ![]() 的最大值为
的最大值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)关于![]() 的方程
的方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若存在![]() ,不等式
,不等式![]() 成立,请同学们探究实数
成立,请同学们探究实数![]() 的所有可能取值.
的所有可能取值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据![]() ,利用
,利用![]() 的最大值为
的最大值为![]() ,可得
,可得![]() ,再根据
,再根据![]() 即可确定
即可确定![]() 的解析式;(2) 关于
的解析式;(2) 关于![]() 的方程
的方程![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 上有解,根据函数单调性的求出
上有解,根据函数单调性的求出![]() 的值域,即可得结果;(3)利用函数奇偶性和单调性之间的关系,可得不等式
的值域,即可得结果;(3)利用函数奇偶性和单调性之间的关系,可得不等式![]() 成立等价于
成立等价于![]() 成立,即存在
成立,即存在![]() 使得
使得![]() 成立,求出
成立,求出![]() 的最小值即可得结果.
的最小值即可得结果.
试题解析:(1)![]() 定义在
定义在![]() 上的奇函数,所以
上的奇函数,所以![]() ,又
,又 易得
易得![]() ,从而,
,从而, ![]() ,所以
,所以![]() ,
, ![]() . 故
. 故![]() .
.
(2)关于![]() 的方程
的方程![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 上有解
上有解
令: ![]() ,则
,则![]() 在
在![]() 上单调性递增函数,
上单调性递增函数,
所以![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
从而,实数![]() 的取值范围
的取值范围![]() .
.
(3)因为![]() 是奇函数且在
是奇函数且在![]() 为单调递增函数,
为单调递增函数,
所以由![]() 有
有![]() ,
,
即:存在![]() 使得
使得![]() 成立,分别由
成立,分别由![]() 以及
以及![]() 在
在![]() 上的图像可知,
上的图像可知, ![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,所以
,所以![]()
又![]() 即
即![]() ,所以
,所以![]() ,综上:
,综上: ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: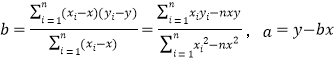 ,).
,).