Question

（09年丰台区期末文）（13分）

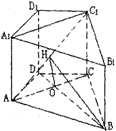
       直四棱柱ABCD―A₁B₁C₁D₁中，∠ADC = 90°，△ABC为等边三角形，且AA₁ = AD = DC

= 2 。

       （Ⅰ）求异面直线AC₁与BC所成的角余弦值；

（Ⅱ）求证：BD⊥平面AC₁；

（Ⅲ）求二面角B―AC₁―C的正切值。

Answer 1

解析：（Ⅰ）在直四棱柱ABCD―A₁B₁C₁D₁中，BC∥B₁C₁

              ∠AC₁B₁是异面直线AC₁与BC所成的角   … 2分

              在△AC₁B₁中，AC₁ = AB₁ =，

              C₁B₁ = ，cos∠AC₁B₁ =

              故    异面直线AC₁与BC所成的角的余弦值为 ………………………… 4分

       （Ⅱ）因为AD = DC ， AB = BC      可得       BD⊥AC（垂直平分线）……… 5分

              又    CC₁⊥平面ABCD，AC为AC₁平面ABCD上的射影 ………………… 7分

              所以       BD⊥AC₁  …………………………………………………………… 8分

       （Ⅲ）设AC∩BD = O，由（Ⅱ）得         BD⊥平面ACC₁，过O作OH⊥AC₁，垂足为

H，连接BH，则BH⊥AC₁，∠OHB为二面角B―AC₁―C的平面角 … 11分

              在Rt△OBH中，OB =，OH =tan∠OHB = 3 ………… 13分

              故    二面角B―AC₁―C的正切值为3