Question

【题目】椭圆 过点 ，离心率为 ，左、右焦点分别为F1 ， F2 ， 过F1的直线交椭圆于A，B两点． （Ⅰ）求椭圆C的方程；
（Ⅱ）当△F2AB的面积为 时，求直线的方程．

Answer 1

【答案】解：（Ⅰ）∵椭圆 过点 ， ∴ ①，
又∵离心率为 ，
∴ ，∴ ②，
联立①②得a2=4，b2=3．
∴椭圆的方程为：
（Ⅱ）①当直线的倾斜角为 时， ，
= = ，不适合题意．
②当直线的倾斜角不为 时，设直线方程l：y=k（x+1），
代入 得：（4k2+3）x2+8k2x+4k2﹣12=0
设A（x1 ， y1），B（x2 ， y2），则 ， ，
∴|AB|= = = ．
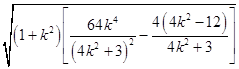点F2到直线l的距离d= ，
∴ = = = ，
化为17k4+k2﹣18=0，解得k2=1，∴k=±1，
∴直线方程为：x﹣y+1=0或x+y+1=0
【解析】（Ⅰ）由于椭圆 过点 ，离心率为 ，可得 ， 即 ，即可解出．（Ⅱ）对直线l的斜率分类讨论，与椭圆的方程联立可得根与系数的关系，再利用弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出．