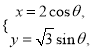题目内容
【题目】已知曲线
的极坐标方程是
,以极点为原点，以极轴为
轴的正半轴，取相同的单位长度，建立平面直角坐标系，直线
的参数方程为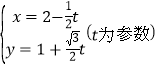
.
（1）写出直线的普通方程与曲线的直角坐标方程；
（2）设曲线经过伸缩变换
得到曲线
，曲线上任一点为
，求
的取值范围．
【答案】（1） 直线
的普通方程为
，曲线
的直角坐标方程为
.
（2）
的取值范围是
.
【解析】
试题（Ⅰ）利用
，将
转化成直角坐标方程，利用消参法法去直线参数方程中的参数
，得到直线的普通方程；（Ⅱ）根据伸缩变换公式求出变换后的曲线方程，然后利用参数方程表示出曲线上任意一点，代入，根据三角函数的辅助角公式求出其范围即可．
试题解析：（Ⅰ）直线的普通方程
曲线的直角坐标方程为
（Ⅱ）曲线经过伸缩变换
得到曲线
的方程为
，即
又点
在曲线上，则
（
为参数）
代入，得
所以的取值范围是
．
【题目】已知椭圆
的左焦点为
，过点
的直线
交椭圆于
两点，
为坐标原点.
（1）若的斜率为
，
为
的中点，且
的斜率为
，求椭圆
的方程；
（2）连结
并延长，交椭圆于点
，若椭圆的长半轴长
是大于的给定常数，求
的面积的最大值
．
【题目】环境问题是当今世界共同关注的问题，我国环保总局根据空气污染指数
溶度，制定了空气质量标准：
某市政府为了打造美丽城市，节能减排，从2010年开始考查了连续六年11月份的空气污染指数，绘制了频率分布直方图，经过分析研究，决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行，即车牌尾号为单号的车辆单号出行，车牌尾号为双号的车辆双号出行（尾号为字母的，前13个视为单号，后13个视为双号）．王先生有一辆车，若11月份被限行的概率为0.05．
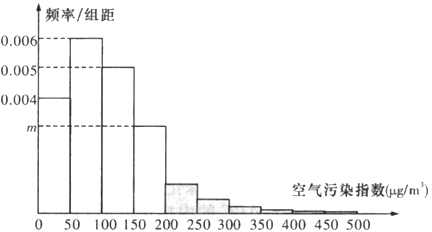
（1）求频率分布直方图中
的值；
（2）若按分层抽样的方法，从空气质量良好与中度污染的天气中抽取6天，再从这6天中随机抽取2天，求至少有一天空气质量中度污染的概率；
（3）该市环保局为了调查汽车尾气排放对空气质量的影响，对限行两年来的11月份共60天的空气质量进行统计，其结果如表：
根据限行前6年180天与限行后60天的数据，计算并填写
列联表，并回答是否有
的把握认为空气质量的优良与汽车尾气的排放有关．
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式：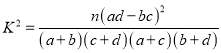 
，其中
．
