题目内容
如图,P1为边长为1的正三角形纸板,在P1的左下端剪去一个边长为
的正三角形得到P2,然后依次剪去一个更小的正三角形(其边长为前一个被剪去的正三角形边长的一半)得到P3,P4,…,Pn,….记纸板Pn的面积记为Sn,则
Sn=

| 1 |
| 2 |
| lim |
| n→∞ |
0
0
.
分析:根据等边三角形的性质(三边相等)求出等边三角形的周长P1,P2,P3,P4,根据周长相减的结果能找到规律即可求出答案.
解答:解:依次剪下去,那边长是以1为首项,
为比例系数的等比数列,
记为bn=(
)n-1,
∴Sn=
×(
)2n-2×sin60°=
•(
)2n-2,
∴
Sn=
[
•(
)2n-2]=0.
故答案为:0.
| 1 |
| 2 |
记为bn=(
| 1 |
| 2 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| ||
| 4 |
| 1 |
| 2 |
故答案为:0.
点评:本题主要考查对等边三角形的性质的理解和掌握,此题是一个规律型的题目,题型较好.

练习册系列答案
相关题目
 “雪花曲线”因其形状类似雪花而得名,它可以以下列方式产生,如图,有一列曲线P1,P2,P3…,,已知P1是边长为1的等边三角形,Pn+1是对Pn进行如下操作得到:将Pn的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(n=1,2,3…).
“雪花曲线”因其形状类似雪花而得名,它可以以下列方式产生,如图,有一列曲线P1,P2,P3…,,已知P1是边长为1的等边三角形,Pn+1是对Pn进行如下操作得到:将Pn的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(n=1,2,3…). 的正三角形得到P2,然后依次剪去一个更小的正三角形(其边长为前一个被剪去的正三角形边长的一半)得到P3,P4,…,Pn,….记纸板Pn的面积记为Sn,则
的正三角形得到P2,然后依次剪去一个更小的正三角形(其边长为前一个被剪去的正三角形边长的一半)得到P3,P4,…,Pn,….记纸板Pn的面积记为Sn,则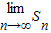 = .
= .