题目内容
数列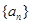 满足
满足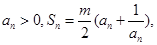 其中
其中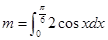 .
.
(I)求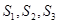 ,猜想
,猜想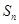 ;(II)请用数学归纳法证明之.
;(II)请用数学归纳法证明之.
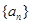 满足
满足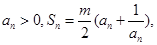 其中
其中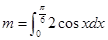 .
.(I)求
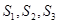 ,猜想
,猜想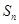 ;(II)请用数学归纳法证明之.
;(II)请用数学归纳法证明之. (1)1, ,
, ,Sn=
,Sn= .(2)见解析.
.(2)见解析.
 ,
, ,Sn=
,Sn= .(2)见解析.
.(2)见解析.第一问中利用数列的赋值思想,由定积分得到 m=1,则可以得到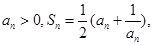 借助于通项公式与前n项和关系求解前几项的和,并猜想得到通项公式。运用数学归纳法加以证明即可。
借助于通项公式与前n项和关系求解前几项的和,并猜想得到通项公式。运用数学归纳法加以证明即可。
解(I) 易得:
∵an>0,∴Sn>0,
由S1= (a1+
(a1+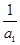 ),变形整理得
),变形整理得 =1,
=1,
取正根得S1=1.
由S2= (a2+
(a2+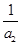 )及a2=S2-S1=S2-1得
)及a2=S2-S1=S2-1得
S2= (S2-1+
(S2-1+ ),变形整理得
),变形整理得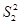 =2,取正根得S2=
=2,取正根得S2= .
.
同理可求得S3=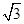 .由此猜想Sn=
.由此猜想Sn= .
.
(II)用数学归纳法证明如下:
(1)当n=1时,上面已求出S1=1,结论成立.
(2)假设当n=k时,结论成立,即Sk=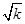 .
.
那么,当n=k+1时,
Sk+1= (ak+1+
(ak+1+ )=
)= (Sk+1-Sk+
(Sk+1-Sk+ )
)
= (Sk+1-
(Sk+1-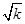 +
+ ).
).
整理得S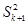 =k+1,取正根得Sk+1=
=k+1,取正根得Sk+1= .
.
故当n=k+1时,结论成立.(11分)
由(1)、(2)可知,对一切n∈N*,Sn= 都成立.
都成立.
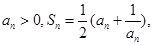 借助于通项公式与前n项和关系求解前几项的和,并猜想得到通项公式。运用数学归纳法加以证明即可。
借助于通项公式与前n项和关系求解前几项的和,并猜想得到通项公式。运用数学归纳法加以证明即可。解(I) 易得:

∵an>0,∴Sn>0,
由S1=
 (a1+
(a1+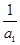 ),变形整理得
),变形整理得 =1,
=1,取正根得S1=1.
由S2=
 (a2+
(a2+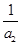 )及a2=S2-S1=S2-1得
)及a2=S2-S1=S2-1得S2=
 (S2-1+
(S2-1+ ),变形整理得
),变形整理得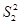 =2,取正根得S2=
=2,取正根得S2= .
.同理可求得S3=
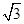 .由此猜想Sn=
.由此猜想Sn= .
.(II)用数学归纳法证明如下:
(1)当n=1时,上面已求出S1=1,结论成立.
(2)假设当n=k时,结论成立,即Sk=
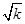 .
.那么,当n=k+1时,
Sk+1=
 (ak+1+
(ak+1+ )=
)= (Sk+1-Sk+
(Sk+1-Sk+ )
)=
 (Sk+1-
(Sk+1-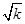 +
+ ).
).整理得S
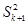 =k+1,取正根得Sk+1=
=k+1,取正根得Sk+1= .
.故当n=k+1时,结论成立.(11分)
由(1)、(2)可知,对一切n∈N*,Sn=
 都成立.
都成立.
练习册系列答案
相关题目

 ;则:(Ⅰ)
;则:(Ⅰ) (Ⅱ)
(Ⅱ) 
 ,
, ,
, ,则可以归纳出
,则可以归纳出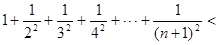 ___.
___.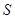 的平面四边形的第
的平面四边形的第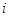 条边的边长记为
条边的边长记为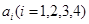 ,
,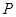 是该四边形内任意一点,
是该四边形内任意一点,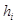 ,若
,若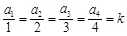 , 则
, 则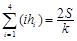 类比上述结论,体积为
类比上述结论,体积为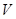 的三棱锥的第
的三棱锥的第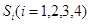 ,
,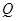 是该三棱锥内的任意一点,
是该三棱锥内的任意一点,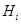 ,则相应的正确命题是:若
,则相应的正确命题是:若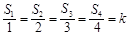 ,则 .
,则 . 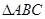 的三边长分别为
的三边长分别为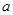 、
、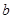 、
、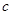 ,其内切圆的半径为
,其内切圆的半径为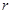 ,则
,则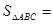
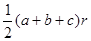 ,类比平几中的这一结论,写出立几中的一个结论为____________.
,类比平几中的这一结论,写出立几中的一个结论为____________.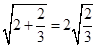 ,
,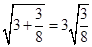 ,
,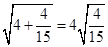 ,。。。,若
,。。。,若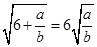 (a , b
(a , b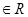 ) , 则a= , b= .
) , 则a= , b= .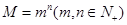 的正整数表示为各项都是整数、公差为2的等差数列的前m项和,称作“对M的m项划分”。例如:
的正整数表示为各项都是整数、公差为2的等差数列的前m项和,称作“对M的m项划分”。例如: 称作“对9的3项划分”;把64表示成
称作“对9的3项划分”;把64表示成 称作“对64的4项划分”.据此,对324的18项划分中最大的数是 ▲
称作“对64的4项划分”.据此,对324的18项划分中最大的数是 ▲