题目内容
12.离心率e=$\frac{1}{2}$,一个焦点是F(3,0)的椭圆标准方程为$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}=1$.分析 利用已知条件求出,椭圆的半长轴与半短轴的长,即可得到椭圆的方程.
解答 解:椭圆的离心率e=$\frac{1}{2}$,一个焦点是F(3,0),可得c=3,a=6,b=$\sqrt{{6}^{2}-{3}^{2}}$=$\sqrt{27}$.
椭圆的标准方程为:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}=1$.
故答案为:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}=1$.
点评 本题考查椭圆的简单性质的应用,椭圆方程的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知a=($\frac{1}{2}$)${\;}^{\frac{2}{3}}$,b=2${\;}^{-\frac{4}{3}}$,c=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$,则下列关系式中正确的是( )
| A. | c<a<b | B. | b<a<c | C. | a<c<b | D. | a<b<c |
3.已知f(x+2)的定义域为[-1,2],则f(2x)的定义域为( )
| A. | [-1,2] | B. | [2,16] | C. | [0,2] | D. | [1,4] |
20.已知函数$f(x)=\left\{{\begin{array}{l}{(a-2)x+1,x<1}\\{{{(\frac{1}{2})}^x}-1,x≥1}\end{array}}\right.$是R上的单调递减函数,则实数a的取值范围是( )
| A. | (-∞,2) | B. | $(-∞,\frac{1}{2}]$ | C. | $[\frac{1}{2},2)$ | D. | (0,2) |
4.函数f(x)=x-ln|x|的图象为( )
| A. |  | B. |  | C. |  | D. |  |
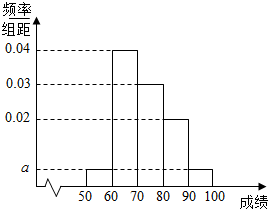 某校高二年级有1200人,从中抽取100名学生,对其期中考试语文成绩进行统计分析,得到如图所示的频率分布直方图,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校高二年级有1200人,从中抽取100名学生,对其期中考试语文成绩进行统计分析,得到如图所示的频率分布直方图,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].