题目内容
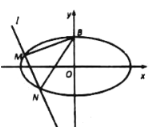
【题目】如图,已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭园C交于
与椭园C交于![]() ,
,![]() 两点,直线
两点,直线![]() 与线
与线![]() 的斜率之积为
的斜率之积为![]() ,证明:直线
,证明:直线![]() 过定点,并求
过定点,并求![]() 的面积
的面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]() 的面积
的面积![]() 的最大值
的最大值![]() .
.
【解析】
(1)求出![]() 后可得椭圆的方程.
后可得椭圆的方程.
(2)设MN:y=kx+m,M(x1,y1),N(x2,y2),与椭圆方程联立化为(1+4k2)x2+8kmx+4m2﹣4=0,△>0.由kBMkBN![]()
利用根与系数的关系代入化简可得:m2+2m﹣3=0,解得m.再求得|MN|,点B到直线MN的距离d,可得S△BMN,通过换元利用基本不等式的性质即可得出.
(1)因为一个顶点为![]() ,故
,故![]() ,又离心为
,又离心为![]() ,故
,故![]() 即
即![]() ,
,
所以![]() ,故椭圆方程为:
,故椭圆方程为:![]() .
.
(2)若直线![]() 的斜率不存在,则设
的斜率不存在,则设![]() ,
,![]()
此时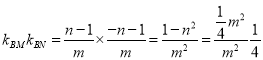 ,与题设条件矛盾,故直线
,与题设条件矛盾,故直线![]() 的斜率必存在.
的斜率必存在.
设MN:y=kx+m,M(x1,y1),N(x2,y2),
联立![]() ,化为(1+4k2)x2+8kmx+4m2﹣4=0,
,化为(1+4k2)x2+8kmx+4m2﹣4=0,
△=16(4k2﹣m2+1)>0,
∴x1+x2![]() ,∴x1x2
,∴x1x2![]() .
.
∵kBMkBN![]()
∴![]() x1x2+k(m﹣1)(x1+x2)+(m﹣1)2=0,
x1x2+k(m﹣1)(x1+x2)+(m﹣1)2=0,
∴![]() k(m﹣1)
k(m﹣1)![]() (m﹣1)2=0,
(m﹣1)2=0,
化为m2+2m﹣3=0,解得m=﹣3或m=1(舍去).
即直线过定点(0,﹣3)
∴|MN|![]()
![]()
点B到直线MN的距离d![]() .
.
∴S△BMN![]() MNd
MNd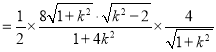 .
.
由m=﹣3,△>0,可知:k2﹣2>0,令![]() t>0,
t>0,
∴k2=t2+2,
∴S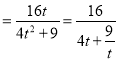 ,当且仅当t
,当且仅当t![]() ,即k=±
,即k=±![]() 时,Smax
时,Smax![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目