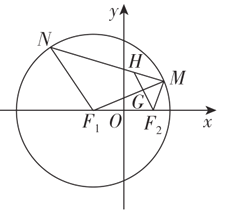
题目内容
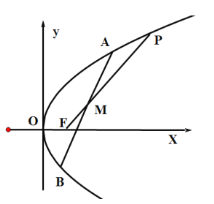
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,且满足
,且满足![]() .
.
(1)若直线![]() 的斜率为1,求点
的斜率为1,求点![]() 的坐标;
的坐标;
(2)若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
(1)由得![]() 抛物线的方程为
抛物线的方程为![]() ,设直线
,设直线![]() 方程为
方程为![]() ,与抛物线方程联立可得到
,与抛物线方程联立可得到![]() 的纵坐标,从而得到点
的纵坐标,从而得到点![]() 的坐标.
的坐标.
(2) 设直线![]() 方程为
方程为![]() ,与抛物线方程联立可得到
,与抛物线方程联立可得到![]() ,又
,又![]() ,可得
,可得![]() ,则可求出
,则可求出![]() 的范围,然后用弦长公式求出
的范围,然后用弦长公式求出![]() 的长,求出点
的长,求出点![]() 到
到![]() 的距离,
的距离,![]() ,然后再求最大值.
,然后再求最大值.
解(1)点![]() 是抛物线的焦点,则抛物线的方程为
是抛物线的焦点,则抛物线的方程为![]() .
.
设直线![]() 方程为
方程为![]() ,
,![]() ,
,![]() ,
,![]()
由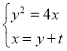 ,得
,得![]() ,
,![]() ,
,![]() ,
,
由![]() 得
得![]()
所以![]() ,
,![]() ,
,![]() .
.
(2)设直线![]() 方程为
方程为![]() .
.
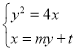 ,得
,得![]() ,
,
从而![]()
 .
.
由于![]() 为线段
为线段![]() 的中点,则
的中点,则![]() ,
,![]() ,即
,即![]()
又![]() ,则
,则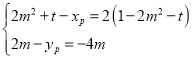 ,从而
,从而![]()
点![]() 在抛物线上,则
在抛物线上,则![]() ,
,![]() .
.
由于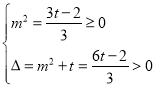 且
且![]() ,得
,得![]() ,
,
又![]() 三点共线时,
三点共线时,![]() ,所以
,所以![]() .
.
又![]()
点![]() 到
到![]() 的距离
的距离![]() ,
,
则![]() ,
,
记![]() ,则
,则![]() .
.
故![]() 在区间
在区间![]() 递减,
递减,![]() 递增,
递增,![]() ,此时
,此时![]()
所以![]()
四边形![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气![]() 数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数![]() 与空气
与空气![]() 数值不合格的天数
数值不合格的天数![]() 进行统计分析,得出下表数据:
进行统计分析,得出下表数据:
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
(1)以统计数据为依据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)求出的线性回归方程,预测该市烧煤取暖的天数为20时空气![]() 数值不合格的天数.
数值不合格的天数.
参考公式: ,
,![]() .
.