Question

（08年朝阳区综合练习一文）（13分）

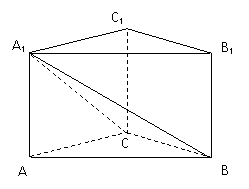
直三棱柱ABC-A₁B₁C₁中，∠ACB=120°，AC=CB=A₁A=1.

（Ⅰ）求证：∥ 平面；

（Ⅱ）求三棱锥A-A₁CB的体积；

（Ⅲ）求二面角A₁-CB-A的正切值.

 

 

 

Answer 1

 解析：方法1：

   （Ⅰ）解：

在三棱柱中C₁B₁∥CB，平面且平面

则∥ 平面.……3分

（Ⅱ）解：因为==×1×(1×1×sin120°)=.…………6分

（Ⅲ）解:

在平面ABC内过点A向BC做垂线AD，

交BC延长线于点D，连结A₁D.

因为A₁A⊥平面ABC，

所以A₁D⊥BD.

所以∠A₁DA是二面角A₁-CB-A的平面角.

容易求出AD=，

所以tan∠A₁DA===.

即二面角A₁-CB-A的正切值是………………………………………………13分

方法2：

如图建立空间直角坐标系，

则有A(1，0，0)，A₁(1，0，1)，B(-，，0)，

B₁(-，，1)，C₁(0，0，1).

 

（Ⅰ）略.

（Ⅱ）略.

（Ⅲ）解：

显然n₁=(0，0，1)是平面ABC的一个法向量.

设n₂=(x，y，z)是平面A₁BC的法向量，

则n₂?=0，且n₂?=0.

即x+z=0，且-x+y=0.

解得平面A₁BC的一个法向量是n₂=(1，，-1).

因为n₁?n₂=-1，| n₁|=1，| n₂|=，

设二面角A₁-CB-A的大小为β，

则cos(π-β)= -= -.所以cosβ=.

所以tanβ=.……………………………………13分