题目内容
已知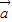 =(
=(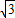 ,cosx),
,cosx),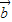 =(cos2x,sinx),函数f(x)=
=(cos2x,sinx),函数f(x)=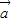 •
•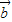 -
-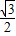 .
.(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若
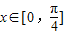 ,求函数f(x)的取值范围;
,求函数f(x)的取值范围;(Ⅲ)函数f(x)的图象经过怎样的平移可使其对应的函数成为奇函数?
【答案】分析:(Ⅰ)欲求函数f(x)的单调递增区间,先利用平面向量点坐标计算公式计算出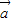
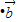 的值,在利用三角函数两角和公式和三角函数的性质求其单调性.
的值,在利用三角函数两角和公式和三角函数的性质求其单调性.
(Ⅱ)根据(Ⅰ)所化简的结果,再根据定义域和三角函数讨论函数的最值.
(Ⅲ)利用图象平移相关知识即可得到结果.
解答:解:(1)函数f(x)=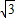 cos2x+sinxcosx
cos2x+sinxcosx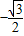 =
=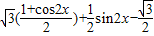 =
=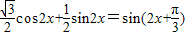
∴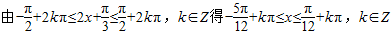
所以f(x)的单调递增区间为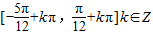 (5分)
(5分)
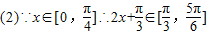
∴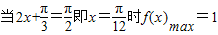
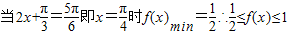
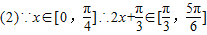
∴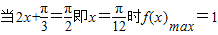
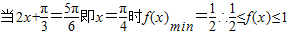
(3)当f(x)的图象上所有的点向右平移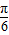 个单位长度得到y=sin2x的图象,则其对应的函数即为奇函数.(12分)
个单位长度得到y=sin2x的图象,则其对应的函数即为奇函数.(12分)
点评:本题考查平面向量的数量积运算,同时考查函数的单调性和奇偶性等相关性质.
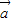
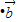 的值,在利用三角函数两角和公式和三角函数的性质求其单调性.
的值,在利用三角函数两角和公式和三角函数的性质求其单调性.(Ⅱ)根据(Ⅰ)所化简的结果,再根据定义域和三角函数讨论函数的最值.
(Ⅲ)利用图象平移相关知识即可得到结果.
解答:解:(1)函数f(x)=
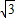 cos2x+sinxcosx
cos2x+sinxcosx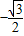 =
=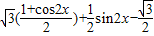 =
=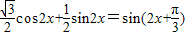
∴
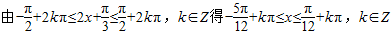
所以f(x)的单调递增区间为
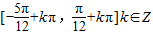 (5分)
(5分)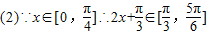
∴
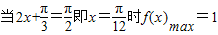
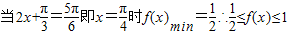
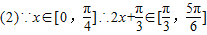
∴
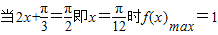
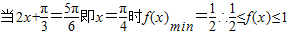
(3)当f(x)的图象上所有的点向右平移
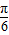 个单位长度得到y=sin2x的图象,则其对应的函数即为奇函数.(12分)
个单位长度得到y=sin2x的图象,则其对应的函数即为奇函数.(12分)点评:本题考查平面向量的数量积运算,同时考查函数的单调性和奇偶性等相关性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目