题目内容
设函数
(Ⅰ) 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ)当 时,设
时,设 的最小值为
的最小值为 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
【答案】
(Ⅰ)
 (Ⅱ)
(Ⅱ)  为所求.
为所求.
【解析】(Ⅰ)利用导数法求得函数的单调区间,求解时需要注意函数的定义域;(Ⅱ)先利用已知把恒成立问题转化为求函数最值问题,然后利用导数法求出函数最值即可
(Ⅰ) ,
┄┄┄┄┄1分
,
┄┄┄┄┄1分
当 时,
时, 解
解


 ┄┄┄┄┄4分
┄┄┄┄┄4分
(Ⅱ)若 ,由
,由 得
得 ,由
,由 得
得 ,
,
所以函数 的减区间为
的减区间为 ,增区间为
,增区间为 ;
;
 ,
┄┄┄┄┄6分
,
┄┄┄┄┄6分
因为 ,所以
,所以 ,
,
令 ,则
,则 恒成立
恒成立
由于 ,当
,当 时,
时, ,故函数
,故函数 在
在 上是减函数,
上是减函数,
所以 成立;
┄┄┄┄┄┄10分
成立;
┄┄┄┄┄┄10分
当 时,若
时,若 则
则 ,故函数
,故函数 在
在 上是增函数,
上是增函数,
即对 时,
时, ,与题意不符;综上,
,与题意不符;综上, 为所求
为所求

练习册系列答案
相关题目

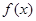 的极值;
的极值; 上是递增函数,求实数a的取值范围;
上是递增函数,求实数a的取值范围; ,求
,求 )是函数
)是函数  (
( )的两个极值点.(I)若
)的两个极值点.(I)若  ,
, ,求函数
,求函数
 的解析式;
的解析式; ,求 b 的最大值;
,求 b 的最大值; ,
, ,当
,当
 时,求
时,求
 的最大值.
的最大值.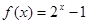 的反函数为
的反函数为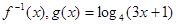
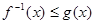 ,求
,求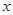 的取值范围D;
的取值范围D; ;当
;当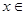 D时,求函数H
D时,求函数H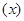 的值域
的值域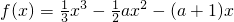
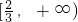 上是递增函数,求实数a的取值范围;
上是递增函数,求实数a的取值范围;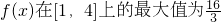 ,求f(x)在该区间上的最小值.
,求f(x)在该区间上的最小值.