题目内容
设函数
①当a=1时,求函数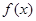 的极值;
的极值;
②若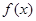 在
在 上是递增函数,求实数a的取值范围;
上是递增函数,求实数a的取值范围;
③当0<a<2时, ,求
,求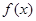 在该区间上的最小值.
在该区间上的最小值.
【答案】
(1) ;(2)
;(2) ;(3)当x=2时取得最小值,为
;(3)当x=2时取得最小值,为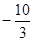 .
.
【解析】(1)求出导数 ,然后根据
,然后根据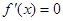 解出极值点,进而根据极值的确定方法求极值即可.
解出极值点,进而根据极值的确定方法求极值即可.
(2)由题意知把此问题转化为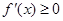 在
在 上恒成立问题解决即可,
上恒成立问题解决即可,
(3) 令 得,
得, ,由于0<a<2,所以当x=1或4时
,由于0<a<2,所以当x=1或4时 有可能取最大值,然后再分类讨论可求出a值.再进一步确定最小值.
有可能取最大值,然后再分类讨论可求出a值.再进一步确定最小值.
解:因为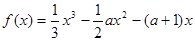
所以 …………………………………………1分
…………………………………………1分
① 因为a=1,所以
所以 …………………………………………2分
…………………………………………2分
令 得,
得, …………………………………………3分
…………………………………………3分
列表如下:
|
x |
|
-1 |
|
2 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
y |
增 |
极大值 |
减 |
极小值 |
增 |
当x=-1时取得极大值,为 ;
;
当x=2时取得极小值,为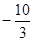 …………………………………………5分
…………………………………………5分
② 因为 在
在 上是递增函数,
上是递增函数,
所以 在
在 上恒成立,…………………………………………6分
上恒成立,…………………………………………6分
即 在
在 上恒成立.
上恒成立.

解得 …………………………………………8分
…………………………………………8分
③令 得,
得,
列表如下:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
y |
减 |
极小值 |
增 |
由上表知当x=1或4时 有可能取最大值,………………………………9分
有可能取最大值,………………………………9分
令 解得a=-4不符合题意舍.…………………………………………10分
解得a=-4不符合题意舍.…………………………………………10分
令 解得a=1…………………………………………11分
解得a=1…………………………………………11分
因为a=1,
所以
令 得,
得, …………………………………………12分
…………………………………………12分
列表如下:
|
x |
|
2 |
|
|
|
- |
0 |
+ |
|
y |
减 |
极小值 |
增 |
当x=2时取得最小值,为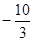 …………………………………………14分
…………………………………………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目









