题目内容
(本小题满分12分)如图5,已知椭圆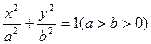 的离心率为
的离心率为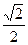 ,其右焦点F是圆
,其右焦点F是圆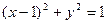 的圆心。
的圆心。
(1)求椭圆方程;
(2)过所求椭圆上的动点P作圆的两条切线分别交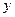 轴于
轴于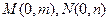 两点,当
两点,当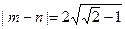 时,求此时点P的坐标。
时,求此时点P的坐标。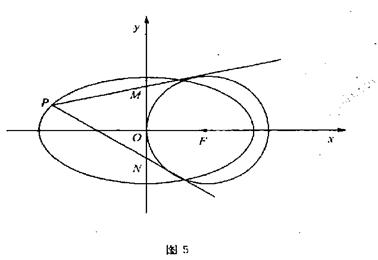
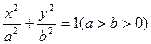 的离心率为
的离心率为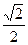 ,其右焦点F是圆
,其右焦点F是圆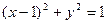 的圆心。
的圆心。(1)求椭圆方程;
(2)过所求椭圆上的动点P作圆的两条切线分别交
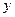 轴于
轴于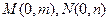 两点,当
两点,当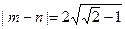 时,求此时点P的坐标。
时,求此时点P的坐标。
(1)椭圆方程为 (2)
(2) 的坐标是
的坐标是
 (2)
(2) 的坐标是
的坐标是
(1)因为圆 的圆心是
的圆心是 ,
,
所以椭圆 的右焦点为
的右焦点为 ,
,
 椭圆的离心率是
椭圆的离心率是 ,
,
 ,所以椭圆方程为
,所以椭圆方程为 。……………………4分
。……………………4分
(2)设 ,
,
由 ,
,
得 或
或 (舍),
(舍),
 .……………………5分
.……………………5分
直线 的方程:
的方程: ,
,
化简得 。
。
又圆心 到直线
到直线 的距离为
的距离为 ,
,

化简得: ,……………………7分
,……………………7分
同理:
 ,
, ……………………9分
……………………9分


 在椭圆上
在椭圆上
 ,……………………11分
,……………………11分
 ,
, (舍)或
(舍)或

所以,此时点 的坐标是
的坐标是 .……………………12分.
.……………………12分.
 的圆心是
的圆心是 ,
,所以椭圆
 的右焦点为
的右焦点为 ,
, 椭圆的离心率是
椭圆的离心率是 ,
,
 ,所以椭圆方程为
,所以椭圆方程为 。……………………4分
。……………………4分(2)设
 ,
,由
 ,
,得
 或
或 (舍),
(舍), .……………………5分
.……………………5分直线
 的方程:
的方程: ,
,化简得
 。
。又圆心
 到直线
到直线 的距离为
的距离为 ,
,

化简得:
 ,……………………7分
,……………………7分同理:

 ,
, ……………………9分
……………………9分

 在椭圆上
在椭圆上
 ,……………………11分
,……………………11分 ,
, (舍)或
(舍)或

所以,此时点
 的坐标是
的坐标是 .……………………12分.
.……………………12分.
练习册系列答案
相关题目
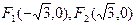 ,离心率
,离心率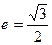 。
。 ,若
,若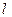 与此椭圆相交于P、Q两点,且
与此椭圆相交于P、Q两点,且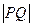 等于椭圆的短轴
等于椭圆的短轴 长,求m的值.
长,求m的值.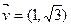 的直线l 过点(
的直线l 过点(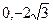 )和椭圆C:
)和椭圆C: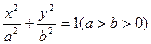 的焦点,且椭圆的中心关于直线l的对称点在椭圆C的右准线上。
的焦点,且椭圆的中心关于直线l的对称点在椭圆C的右准线上。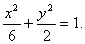
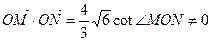 (O为原点),若存在求出直线的方程,若不存在,请说明理由。
(O为原点),若存在求出直线的方程,若不存在,请说明理由。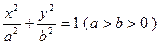 ,它的一个顶点为
,它的一个顶点为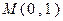 ,离心率
,离心率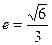 .
.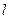 与椭圆交于A,B两点,坐标原点O到直线l的距离为
与椭圆交于A,B两点,坐标原点O到直线l的距离为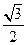 ,求△AOB面积的最大值.
,求△AOB面积的最大值.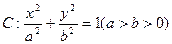 的左、右焦点分别为F1与F2,直线
的左、右焦点分别为F1与F2,直线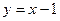 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若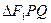 的周长为
的周长为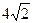 。
。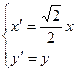 变成曲线
变成曲线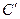 ,直线
,直线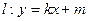 与曲线
与曲线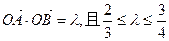 ,求
,求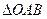 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 的方程是
的方程是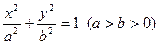 ,椭圆的左顶点为
,椭圆的左顶点为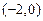 ,离心率
,离心率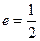 ,倾斜角为
,倾斜角为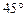 的直线
的直线 与椭圆交于
与椭圆交于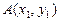 、
、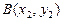 两点.
两点. (
(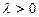 ),若点
),若点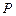 在椭圆
在椭圆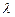 的取值范围.
的取值范围.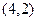 是直线
是直线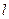 被椭圆
被椭圆 所截得的线段的中点,则
所截得的线段的中点,则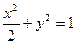 的右焦点为F,右准线为l,点
的右焦点为F,右准线为l,点 ,线段AF交椭圆C于点B,若
,线段AF交椭圆C于点B,若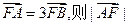 =" " ( )
=" " ( )
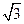
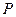 是以
是以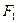 ,
,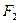 为焦点的椭圆
为焦点的椭圆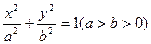 上的一点,若
上的一点,若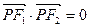 ,
,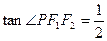 ,则此椭圆的离心率为____________.
,则此椭圆的离心率为____________.