题目内容

在三棱锥S-ABC中，AB⊥BC，AB=BC=
2
，SA=SC=2，，二面角S-AC-B的余弦值是-
3
3
，若S、A、B、C都在同一球面上，则该球的表面积是（　　）
分析：由AB⊥BC，得△ABC的外接圆的圆心O′为AC中点，连接SO′，BO′，可证OO′⊥底面ABC，将平面SO′B取出，求出SB，作SB的中垂线，过O′作BO′的垂线，两者必相交于O，用余弦定理，求得cos∠O′BS，从而可知D，E，O三点重合了
，可得外接圆的半径，即可求得球的表面积．
解答：解：由AB⊥BC，得△ABC的外接圆的圆心O′为AC中点，连接SO′，BO′，由SA=SC和AB=BC有SO′⊥AC，BO′⊥AC
而四面体外接球的球心O在平面SO′B内，连接OO′，有OO′⊥底面ABC
将平面SO′B取出，则BO′=1，SO′=
3

用余弦定理可得cos∠SO′B=-
3
3

∴SB=
6

作SB的中垂线，过O′作BO′的垂线，两者必相交于O，用余弦定理，cos∠O′BS=
6
3

如图，BE=O′B÷cos∠O′BS=
6
2
=
SB
2

也就是D，E，O三点重合了
外接圆的半径R=OB=
6
2

∴球的表面积是4πR2=6π
故选D．
点评：本题考查面面角，考查球的表面积，解题的关键是确定外接圆的半径，属于中档题．
练习册系列答案
相关题目
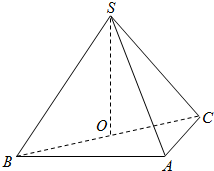精英家教网如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为边长为1的等边三角形，∠BAC=90°，O为BC中点．
（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）证明：SA⊥BC；
（Ⅲ）求三棱锥S-ABC的体积．
精英家教网如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC=90°，O为BC中点．
（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）求二面角A-SC-B的余弦值．
精英家教网如图，在三棱锥S-ABC中，侧面SAB⊥底面ABC，且∠ASB=∠ABC=90°，AS=SB=2，AC=2
3
．

（Ⅰ）求证SA⊥SC；
（Ⅱ）在平面几何中，推导三角形内切圆的半径公式r=
2S
l
（其中l是三角形的周长，S是三角形的面积），常用如下方法（如右图）：
①以内切圆的圆心O为顶点，将三角形ABC分割成三个小三角形：△OAB，△OAC，△OB精英家教网C．
②设△ABC三边长分别为a，b，c．由S△ABC=S△OBC+S△OAC+S△OAB，
得S=
1
2
ar+
1
2
br+
1
2
cr=
1
2
lr，则r=
2S
l
．
类比上述方法，请给出四面体内切球半径的计算公式（不要求说明类比过程），并利用该公式求出三棱锥S-ABC内切球的半径．
如图，在三棱锥S-ABC中，SA=AB=BC=AC=
2
SB=
2
SC，O为BC中点．
（1）求证：SO⊥平面ABC
（2）在线段AB上是否存在一点E，使二面角B-SC-E的平面角的余弦值为
15
5
？若存在，确定E点位置；若不存在，说明理由．
在三棱锥S-ABC中，侧棱SC⊥平面SAB，SA⊥BC，侧面△SAB，△SBC，△SAC的面积分别为1，
3
2
，3，则此三棱锥的外接球的表面积为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网