题目内容
 如图,棱长为1的正方体ABCD-A1B1C1D1中,P为AD1中点
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为AD1中点
(I)求三棱锥C-PDB的体积
(II)在对角线A1C上是否存在一点Q,使得AD1∥平面QBD,若存在,求出 ;若不存在,说明理由.
;若不存在,说明理由.
解:(I)∵P为AD1中点
故P点到底面ABCD的距离等于棱长的一半
又∵S△BCD=
∵VC-PDB=CP-BCD= =
= ;
;
(II)连接BC1,DC1,
∵AD1∥BC1,
∴AD1∥平面BDC1,
令A1C∩平面BDC1=Q
由正方体的几何特征易得A1C⊥平面BDC1,
且A1Q=2QC
故 =2
=2
分析:(I)由已知中棱长为1的正方体ABCD-A1B1C1D1中,P为AD1中点,则VC-PDB=CP-BCD,求出棱锥的高和底面面积,代入棱锥体积公式即可求出答案;
(II)连接BC1,DC1,由线面平行的判定定理,易得AD1∥平面BDC1,则直线A1C与平面BDC1的交点即为Q,根据正方体的性质易得到 的值.
的值.
点评:本题考查的知识点是直线与平面平行的判定与性质,三棱锥的体积,其中(1)的关键是利用等体积法将求三棱锥C-PDB的体积,转化为求三棱锥P-CDB的体积,(II)的关键是找到满足条件的Q点的位置.
故P点到底面ABCD的距离等于棱长的一半

又∵S△BCD=

∵VC-PDB=CP-BCD=
 =
= ;
;(II)连接BC1,DC1,
∵AD1∥BC1,
∴AD1∥平面BDC1,
令A1C∩平面BDC1=Q
由正方体的几何特征易得A1C⊥平面BDC1,
且A1Q=2QC
故
 =2
=2分析:(I)由已知中棱长为1的正方体ABCD-A1B1C1D1中,P为AD1中点,则VC-PDB=CP-BCD,求出棱锥的高和底面面积,代入棱锥体积公式即可求出答案;
(II)连接BC1,DC1,由线面平行的判定定理,易得AD1∥平面BDC1,则直线A1C与平面BDC1的交点即为Q,根据正方体的性质易得到
 的值.
的值.点评:本题考查的知识点是直线与平面平行的判定与性质,三棱锥的体积,其中(1)的关键是利用等体积法将求三棱锥C-PDB的体积,转化为求三棱锥P-CDB的体积,(II)的关键是找到满足条件的Q点的位置.

练习册系列答案
相关题目
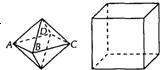


 两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
两个相同的正四棱锥组成如图所示的几何体,可放入棱长为