题目内容
10.已知函数f(x)=x2-kx-2在区间(1,5)上既没有最大值也没有最小值,则实数k的取值范围是( )| A. | [10,+∞) | B. | (-∞,2] | C. | (-∞,2]∪[10,+∞) | D. | (-∞,1]∪[5,+∞) |
分析 两条二次函数的对称轴与求解的关系列出不等式求解即可.
解答 解:由函数f(x)=x2-kx-2,可知函数的对称轴为:x=$\frac{k}{2}$,
函数f(x)=x2-kx-2在区间(1,5)上既没有最大值也没有最小值,
可得$\frac{k}{2}≤1$或$\frac{k}{2}≥5$,解得k∈(-∞,2]∪[10,+∞).
故选:C.
点评 本题考查二次函数的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(0≤x≤1)}\\{f(x-1)+m(x>1)}\end{array}\right.$在定义域[0,+∞)上单调递增,且对于任意a≥0,方程f(x)=a有且只有一个实数解,则函数g(x)=f(x)-x在区间[0,2n](n∈N*)上所有零点的和为( )
| A. | $\frac{n(n+1)}{2}$ | B. | 22n-1+2n-1 | C. | $\frac{(1+{2}^{n})^{2}}{2}$ | D. | 2n-1 |
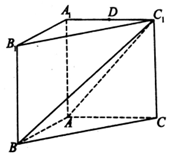 如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C
如图,直三棱柱ABC-A1B1C1中,AC=AA1=2AB,且BC1⊥A1C