题目内容

椭圆与双曲线的离心率互为倒数，左焦点到直线的距离为。

   （Ⅰ）求椭圆M的方程。

   （Ⅱ）若直线l与垂直，且与椭圆M有且仅有一个公共点，求直线l的方程。

(I)由x2-y2=即得

    ∵因为椭圆M的离心率与互为倒数,∴椭圆的离心率为．

       

又F(-c,0)到直线x+y-b=0的距离为

,,

      

(Ⅱ)∵直线l与x+y-b=0垂直,∴设l:x-y+m=0

     由 得

  ∵l与M有且仅有一个公共点，∴△=16m2-4×3×2(m2-1)=0，解得：m=±

      ∴

练习册系列答案
相关题目
精英家教网如图，在中△ABC，∠CBA=∠CAB=30°，AC、BC边上的高分别为BD、AE，则以A、B为焦点，且过D、E的椭圆与双曲线的离心率的倒数和为（　　）
A、
3
B、1
C、2
3
D、2
（2008•和平区三模）如图，在△ABC中，∠ABC=∠ACB=30°，AB，AC边上的高分别为CD，BE，则以B，C为焦点且经过D、E两点的椭圆与双曲线的离心率的和为
2
3
2
3
．
已知双曲线与椭圆
x2
4
+y2=1共焦点，它们的离心率之和为
3
3
2
；
（1）求椭圆与双曲线的离心率e1、e2；
（2）求双曲线的标准方程与渐近线方程；
（3）已知直线l：y=
1
2
x+m与椭圆有两个交点，求m的取值范围．
已知椭圆
x2
2a2
+
y2
b2
=1(a＞b＞0)和双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)，有相同的焦点，则椭圆与双曲线的离心率的平方和为（　　）
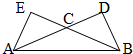精英家教网如图，在△ABC中，∠CAB=∠CBA=30°，AC、BC边上的高分别为BD、AE，垂足分别是D、E，则以A、B为焦点且过D、E的椭圆与双曲线的离心率分别为e1、e2，则
1
e1
+
1
e2
的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网