题目内容
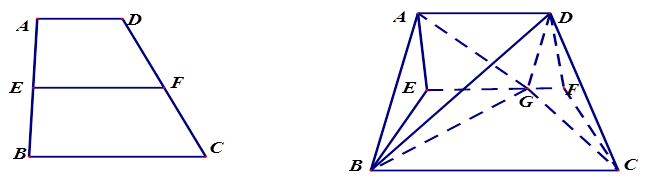
如图,在直三棱柱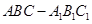 (侧棱和底面垂直的棱柱)中,
(侧棱和底面垂直的棱柱)中,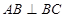 ,
,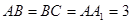 ,
,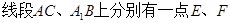 ,且满足
,且满足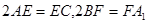 .
.
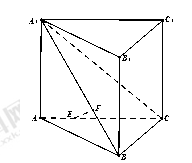
(1)求证:平面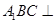 侧面
侧面 ;
;
(2)求二面角 的平面角的余弦值。
的平面角的余弦值。
 (侧棱和底面垂直的棱柱)中,
(侧棱和底面垂直的棱柱)中,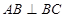 ,
,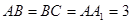 ,
,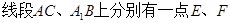 ,且满足
,且满足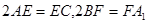 .
.
(1)求证:平面
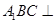 侧面
侧面 ;
;(2)求二面角
 的平面角的余弦值。
的平面角的余弦值。(1)详见解析;(2)

试题分析:(1)可证
 得面
得面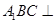 侧面
侧面 (2)此问采用空间向量法较好。先建系,写出个点坐标,再给出各向量的坐标,分别求面
(2)此问采用空间向量法较好。先建系,写出个点坐标,再给出各向量的坐标,分别求面 和面
和面 的法向量。先求得两法向量所成角的余弦值,但两法向量所成的角和二面角相等或互补,观察可知此二面角为顿角,所以余弦值为负值。
的法向量。先求得两法向量所成角的余弦值,但两法向量所成的角和二面角相等或互补,观察可知此二面角为顿角,所以余弦值为负值。试题解析:(1)证明:
 ,
,

又

 4分
4分(2)由(Ⅰ)知,以点
 为坐标原点,以
为坐标原点,以 所在的直线分
所在的直线分别为
 轴、
轴、 轴、
轴、 轴,可建立如图所示的空间直角坐标系,
轴,可建立如图所示的空间直角坐标系,
 ,
,  ,
,  ,
, 
又由线段
 上分别有一点
上分别有一点 ,
,满足
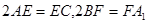 ,
,所以E(1,2,0), F(0,1,1) 6分

 面
面 的一个法向量
的一个法向量 8分
8分此时面
 的一个法向量为
的一个法向量为 ,则
,则 。
。设所求二面角平面角为
 ,观察可知
,观察可知 为钝角,
为钝角,则
 。 12分
。 12分
练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
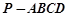 的底面ABCD是平行四边形,
的底面ABCD是平行四边形,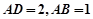 ,
,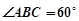 ,
,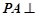 面
面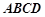 ,设
,设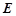 为
为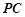 中点,点
中点,点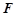 在线段
在线段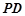 上且
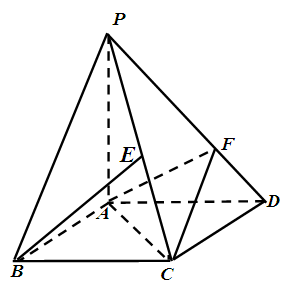
上且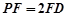 .
.
 平面
平面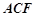 ;
;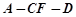 的大小为
的大小为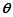 ,若
,若 ,求
,求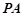 的长.
的长.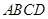 中,
中,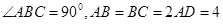 ,点
,点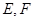 分别是
分别是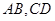 的中点,点
的中点,点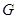 在
在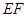 上,沿
上,沿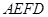
 平面
平面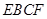 .
.
 最小时,求证:
最小时,求证: ;
; 时,求二面角
时,求二面角 平面角的余弦值.
平面角的余弦值.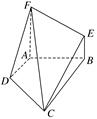
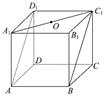
 =
= ,N为B1B的中点,则|
,N为B1B的中点,则| |为( )
|为( ) a
a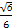 a
a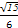 a
a a
a 关于
关于 轴的对称点的坐标为 ( )
轴的对称点的坐标为 ( )


